
分析 (1)通过放缩、裂项可知$\frac{{a}_{n+1}}{{a}_{n}}$>1+$\frac{1}{n}$-$\frac{1}{n+1}$,计算第二项a2并利用数列{an}为递增数列即得结论;
(2)通过(1)放缩可知当n≥2时an+1<(1+$\frac{1}{{n}^{2}+n}$)an+$\frac{1}{{2}^{n+1}}$an,进而整理可知bn<$\frac{1}{n}$-$\frac{1}{n+1}$+$\frac{1}{{2}^{n+1}}$(n≥2),计算即得结论.
解答 证明:(1)依题意,an+1>(1+$\frac{1}{{n}^{2}+n}$)an,
整理得:$\frac{{a}_{n+1}}{{a}_{n}}$>1+$\frac{1}{{n}^{2}+n}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$,即数列{an}为递增数列,
∵a1=1,
∴a2=(1+$\frac{1}{2}$)a1+$\frac{1}{2}$=2,
∴当n≥2时,an≥2;
(2)由(1)可知当n≥2时,an+1<(1+$\frac{1}{{n}^{2}+n}$)an+$\frac{1}{{2}^{n+1}}$an,
∴bn=$\frac{{a}_{n+1}-{a}_{n}}{{a}_{n}}$<$\frac{1}{n}$-$\frac{1}{n+1}$+$\frac{1}{{2}^{n+1}}$(n≥2),
当n=1时,S1=$\frac{2-1}{1}$=1<$\frac{7}{4}$,
当n≥2时,Sn<1+($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)+($\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n+1}}$)
=1+$\frac{1}{2}$-$\frac{1}{n+1}$+$\frac{\frac{1}{{2}^{3}}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$
=$\frac{7}{4}$-$\frac{1}{n+1}$-$\frac{1}{{2}^{n+1}}$
<$\frac{7}{4}$.
点评 本题考查数列的通项及前n项和,考查放缩法,考查裂项相消法,注意解题方法的积累,属于难题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{11}{10}$ | C. | $\frac{13}{14}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
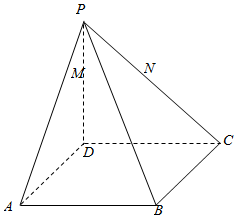 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com