
分析 (Ⅰ)由题意得c=3,2a+2c=16,由此能求出椭圆的方程.
(Ⅱ)由$\left\{\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ y=\frac{{\sqrt{2}}}{4}x\end{array}\right.$,得$({b^2}+\frac{1}{8}{a^2}){x^2}-{a^2}{b^2}=0$.由此利用韦达定理、AB、EF互相平分且共圆,向量的数量积,结合已知条件能求出离心率.
(Ⅲ)由椭圆方程为$\frac{x^2}{12}+\frac{y^2}{3}=1$,设A(x1,y1),B(-x1,-y1),求出${k_1}{k_2}=\frac{{{y_0}^2-{y_1}^2}}{{{x_0}^2-{x_1}^2}}$,由此能求出直线PB的斜率k2的取值范围.
解答 解:(Ⅰ)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右焦点分别为F1,F2,且|F1F2|=6,直线y=kx与椭圆交于A,B两点.
∴由题意得c=3,…(1分)根据2a+2c=16,得a=5. …(2分)
结合a2=b2+c2,解得a2=25,b2=16.…(3分)
∴椭圆的方程为$\frac{x^2}{25}+\frac{y^2}{16}=1$. …(4分)
(Ⅱ)(解法一)由$\left\{\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ y=\frac{{\sqrt{2}}}{4}x\end{array}\right.$,得$({b^2}+\frac{1}{8}{a^2}){x^2}-{a^2}{b^2}=0$.
设A(x1,y1),B(x2,y2).则${x_1}+{x_2}=0,{x_1}{x_2}=\frac{{-{a^2}{b^2}}}{{{b^2}+\frac{1}{8}{a^2}}}$,…(6分)
由AB、EF互相平分且共圆,∴AF2⊥BF2,
∵$\overrightarrow{{F_2}A}=({x_1}-3,{y_1})$,$\overrightarrow{{F_2}B}=({x_2}-3,{y_2})$,
∴$\overrightarrow{{F_2}A}•\overrightarrow{{F_2}B}=({x_1}-3)({x_2}-3)+{y_1}{y_2}=(1+\frac{1}{8}){x_1}{x_2}+9=0$.
即 x1x2=-8,∴$\frac{{-{a^2}{b^2}}}{{{b^2}+\frac{1}{8}{a^2}}}=-8$,
结合b2+9=a2.解得a2=12,∴离心率$e=\frac{{\sqrt{3}}}{2}$. …(8分)
(若设A(x1,y1),B(-x1,-y1)相应给分)
(Ⅲ)由(Ⅱ)结论,椭圆方程为$\frac{x^2}{12}+\frac{y^2}{3}=1$,…(9分)
由题可设A(x1,y1),B(-x1,-y1),${k_1}=\frac{{{y_0}-{y_1}}}{{{x_0}-{x_1}}},{k_2}=\frac{{{y_0}+{y_1}}}{{{x_0}+{x_1}}}$,
∴${k_1}{k_2}=\frac{{{y_0}^2-{y_1}^2}}{{{x_0}^2-{x_1}^2}}$,…(10分)
又$\frac{{{y_0}^2-{y_1}^2}}{{{x_0}^2-{x_1}^2}}=\frac{{3(1-\frac{{{x_0}^2}}{12})-3(1-\frac{{{x_1}^2}}{12})}}{{{x_0}^2-{x_1}^2}}=-\frac{1}{4}$,即${k_2}=-\frac{1}{{4{k_1}}}$,
由-2<k1<-1可知,$\frac{1}{8}<{k_2}<\frac{1}{4}$.…(12分)
点评 本题考查椭圆的标准方程的求法,考查椭圆的离心率和直线的斜率的取值范围的求法,是中档题,解题时要认真审题,注意直线与椭圆的相交综合问题的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| 支持新教材 | 支持旧教材 | 合计 | |
| 教龄在10年以上的教师 | 12 | 34 | 46 |
| 教龄在10年以下的教师 | 22 | 23 | 45 |
| 合计 | 34 | 57 | 91 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.001的前提下,认为“教龄的长短与支持新教材有关” | |
| B. | 在犯错误的概率不超过0.05的前提下,认为“教龄的长短与支持新教材有关” | |
| C. | 在犯错误的概率不超过0.010的前提下,认为“教龄的长短与支持新教材有关” | |
| D. | 我们没有理由认为“教龄的长短与支持新教材有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
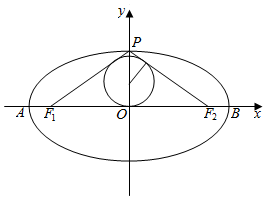 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com