
分析 (1)求得f(x)的导数,由题意可得f′(x)≤0恒成立,即为-b≤ex-2x,令g(x)=ex-2x,求得导数,单调区间,可得极小值,且为最小值,即可得到b的范围;
(2)求得f(x)的解析式,令f(x)=0,可得-a=$\frac{{x}^{2}}{{e}^{x}}$,设h(x)=$\frac{{x}^{2}}{{e}^{x}}$,求得h(x)的导数和单调区间、极值,结合零点个数只有一个,即可得到a的范围;
(3)假设存在实数x0(x0≠m),使得f(x0)=f′($\frac{{x}_{0}+m}{2}$)(x0-m)+n成立.求得f(x)的导数,化简整理可得$\frac{{e}^{{x}_{0}}-{e}^{m}}{{x}_{0}-m}$=e${\;}^{\frac{{x}_{0}+m}{2}}$,考虑函数y=ex的图象与y=lnx的图象关于直线y=x对称,上式可转化为$\frac{ln{x}_{0}-lnm}{{x}_{0}-m}$=$\frac{2}{{x}_{0}+m}$,设t=$\frac{{x}_{0}}{m}$>1,上式即为lnt=$\frac{2(t-1)}{t+1}$,令m(t)=lnt-$\frac{2(t-1)}{t+1}$,t>1,求出导数,判断单调性即可判断不存在.
解答 解:(1)函数f(x)=-ex+x2-bx的导数为f′(x)=-ex+2x-b,
函数y=f(x)在R上是单调减函数,可得f′(x)≤0恒成立,
即为-b≤ex-2x,令g(x)=ex-2x,
g′(x)=ex-2,当x>ln2时,g′(x)>0,g(x)递增;
当x<ln2时,g′(x)<0,g(x)递减.
则g(x)在x=ln2处取得极小值,且为最小值2-2ln2,
即有-b≤2-2ln2,即b≥2ln2-2,
则b的取值范围是[2ln2-2,+∞);
(2)由b=0,可得f(x)=a•ex+x2,
令f(x)=0,即有-a=$\frac{{x}^{2}}{{e}^{x}}$,
设h(x)=$\frac{{x}^{2}}{{e}^{x}}$,h′(x)=$\frac{x(2-x)}{{e}^{x}}$,
当0<x<2时,h′(x)>0,h(x)在(0,2)递增;
当x>2或x<0时,h′(x)<0,h(x)在(-∞,0),(2,+∞)递减.
可得h(x)在x=2处取得极大值$\frac{4}{{e}^{2}}$,
且h(x)>0,x→+∞,h(x)→0,
由题意函数y=f(x)在R上有且只有一个零点,
则-a=0或-a>$\frac{4}{{e}^{2}}$,
即为a=0或a<-$\frac{4}{{e}^{2}}$,即a的取值范围是{0}∪(-∞,-$\frac{4}{{e}^{2}}$);
(3)假设存在实数x0(x0≠m),使得f(x0)=f′($\frac{{x}_{0}+m}{2}$)(x0-m)+n成立.
函数f(x)=a•ex+x2-bx的导数为f′(x)=aex+2x-b,
可得a•ex0+x02-bx0=(ae${\;}^{\frac{{x}_{0}+m}{2}}$+x0+m-b)(x0-m)+a•em+m2-bm,
化简可得(x0-m)($\frac{a({e}^{{x}_{0}}-{e}^{m})}{{x}_{0}-m}$+x0+m-b)=(ae${\;}^{\frac{{x}_{0}+m}{2}}$+x0+m-b)(x0-m),
由a≠0,x0≠m,可得$\frac{{e}^{{x}_{0}}-{e}^{m}}{{x}_{0}-m}$=e${\;}^{\frac{{x}_{0}+m}{2}}$,
上式的几何意义为函数y=ex图象上两点的斜率等于中点处的切线的斜率,
考虑函数y=ex的图象与y=lnx的图象关于直线y=x对称,
上式可转化为$\frac{ln{x}_{0}-lnm}{{x}_{0}-m}$=$\frac{2}{{x}_{0}+m}$,
设x0>m>0,即有lnx0-lnm=$\frac{2({x}_{0}-m)}{{x}_{0}+m}$,即ln$\frac{{x}_{0}}{m}$=$\frac{2(\frac{{x}_{0}}{m}-1)}{\frac{{x}_{0}}{m}+1}$,
设t=$\frac{{x}_{0}}{m}$>1,上式即为lnt=$\frac{2(t-1)}{t+1}$,
令m(t)=lnt-$\frac{2(t-1)}{t+1}$,t>1,则m′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
则m(t)在(1,+∞)递增,
即有m(t)>m(1)=0,则方程lnt=$\frac{2(t-1)}{t+1}$无实数解.
即有$\frac{ln{x}_{0}-lnm}{{x}_{0}-m}$=$\frac{2}{{x}_{0}+m}$不成立,
则$\frac{{e}^{{x}_{0}}-{e}^{m}}{{x}_{0}-m}$=e${\;}^{\frac{{x}_{0}+m}{2}}$不成立.
故不存在实数x0(x0≠m),使得f(x0)=f′($\frac{{x}_{0}+m}{2}$)(x0-m)+n成立.
点评 本题考查导数的运用:求单调区间和极值、最值,考查函数的零点的判断和不等式恒成立问题的解法,以及存在性问题的解法,注意运用转化思想,考查化简整理的运算能力,具有一定的难度.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
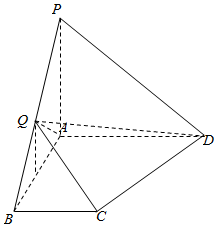 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=90°,AB=AD=AP=2,BC=1.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=90°,AB=AD=AP=2,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
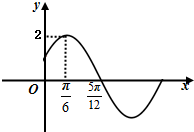 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com