
分析 (1)由三角恒等变换化简f(x),由此得到函数的频率和初相.
(2)由题意得到$A=\frac{π}{3}$,由正弦定理得到$a=\sqrt{6}$,由三角形面积公式得到答案.
解答 解:(1)∵$f(x)=2\sqrt{2}sin\frac{1}{8}xcos\frac{1}{8}x+2\sqrt{2}s{cos^2}\frac{1}{8}x-\sqrt{2}$,
=2$\sqrt{2}$sin$\frac{x}{8}$cos$\frac{x}{8}$+$\sqrt{2}$(2cos2$\frac{x}{8}$-1),
=$\sqrt{2}$sin$\frac{x}{4}$+$\sqrt{2}$cos$\frac{x}{4}$
=2sin($\frac{x}{4}$+$\frac{π}{4}$),
∴函数的频率$f=\frac{1}{T}=\frac{{\frac{1}{4}}}{2π}=\frac{1}{8π}$,
初相为$\frac{π}{4}$,
(2)∵在△ABC中,$f(A)=\sqrt{3}$,
∴$2sin(\frac{1}{4}A+\frac{π}{4})=\sqrt{3}$,
∴$sin(\frac{1}{4}A+\frac{π}{4})=\frac{{\sqrt{3}}}{2}$,
∵0<A<π,
∴$\frac{π}{4}<\frac{1}{4}A+\frac{π}{4}<\frac{π}{2}$,$\frac{1}{4}A+\frac{π}{4}=\frac{π}{3}$,$A=\frac{π}{3}$,
∴$B=π-A-C=\frac{5π}{12}$,
又由正弦定理得$\frac{a}{{sin\frac{π}{3}}}=\frac{c}{{sin\frac{π}{4}}}$,解得 $a=\sqrt{6}$,
∴${S_{△ABC}}=\frac{1}{2}acsinB=\frac{1}{2}•2•\sqrt{6}•\frac{{\sqrt{6}+\sqrt{2}}}{4}=\frac{{3+\sqrt{3}}}{2}$.
点评 本题考查由三角恒等变换,正弦定理以及三角形面积公式.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
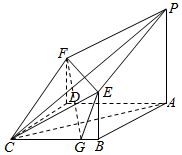 如图所示的几何体由平面PECF截棱长为2的正方体得到,其中P、C为原正方体的顶点,E、F为原正方体侧棱的中点,正方形ABCD为原正方体的底面,点G为线段BC上的动点.
如图所示的几何体由平面PECF截棱长为2的正方体得到,其中P、C为原正方体的顶点,E、F为原正方体侧棱的中点,正方形ABCD为原正方体的底面,点G为线段BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图四棱锥P-ABCD,三角形ABC为正三角形,边长为2,AD⊥DC,AD=1,PO垂直于平面ABCD于O,O为AC的中点.
如图四棱锥P-ABCD,三角形ABC为正三角形,边长为2,AD⊥DC,AD=1,PO垂直于平面ABCD于O,O为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0,1 | B. | 0,2 | C. | 1,2 | D. | 1,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com