
分析 求出f(x)的导数,问题转化为f′(x)≥0在(1,+∞)上恒成立,分离参数,求出a的最小值;求出g(x)的导数,问题转化为a≤[ex]min在区间(1,+∞)上成立,求出a的范围,取交集即可.
解答 解:∵f(x)=ax-lnx,(x>0),
f′(x)=a-$\frac{1}{x}$=$\frac{ax-1}{x}$,
若f(x)在(1,+∞)上无最小值,
则f(x)在(1,+∞)单调,
∴f′(x)≥0在(1,+∞)上恒成立,
或f′(x)≤0在(1,+∞)上恒成立,
∴a≥$\frac{1}{x}$,或a≤$\frac{1}{x}$,而函数y=$\frac{1}{x}$在(1,+∞)上单调减,
∴x=1时,函数y取得最大值1,
∴a≥1或a≤0,而a为正实数,
故a≥1①,
又∵g(x)=ex-ax,
∴g′(x)=ex-a,
∵函数g(x)=ex-ax在区间(1,+∞)上单调递增,
∴函数g′(x)=ex-a≥0在区间(1,+∞)上恒成立,
∴a≤[ex]min在区间(1,+∞)上成立.
而ex>e,
∴a≤e②;
综合①②,a∈[1,e],
故答案为:[1,e].
点评 正确把问题等价转化、熟练掌握利用导数研究函数的单调性、极值与最值等是解题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{e}$ | B. | 1 | C. | e+1 | D. | e-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
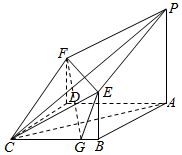 如图所示的几何体由平面PECF截棱长为2的正方体得到,其中P、C为原正方体的顶点,E、F为原正方体侧棱的中点,正方形ABCD为原正方体的底面,点G为线段BC上的动点.
如图所示的几何体由平面PECF截棱长为2的正方体得到,其中P、C为原正方体的顶点,E、F为原正方体侧棱的中点,正方形ABCD为原正方体的底面,点G为线段BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com