
【题目】已知函数f(x)=[ax2﹣(2a+1)x+a+2]ex(a∈R).
(1)当a≥0时,讨论函数f(x)的单调性;
(2)设g(x)= ![]() ,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
【答案】
(1)解:f′(x)=(ax2﹣x﹣a+1)ex=(ax+a﹣1)(x﹣1)ex,
a=0时,f′(x)=﹣(x﹣1)ex,
∴当x>1时,f′(x)<0,函数f(x)单调递减;当x<1时,f′(x)>0,函数f(x)单调递增.
当a>0时,f′(x)=a ![]() (x﹣1)ex,
(x﹣1)ex,
令 ![]() =1,解得a=
=1,解得a= ![]() .
.
当a= ![]() 时,
时, ![]() ≥0,函数f(x)在R上单调递增;
≥0,函数f(x)在R上单调递增;
当 ![]() 时,
时, ![]() >1,x∈(﹣∞,1)时,f′(x)>0,函数f(x)单调递增;
>1,x∈(﹣∞,1)时,f′(x)>0,函数f(x)单调递增; ![]() ,f′(x)<0,函数f(x)单调递减;
,f′(x)<0,函数f(x)单调递减; ![]() ,f′(x)>0,函数f(x)单调递增.
,f′(x)>0,函数f(x)单调递增.
当a ![]() 时,
时, ![]() <1,x∈(﹣∞,
<1,x∈(﹣∞, ![]() )时,f′(x)>0,函数f(x)单调递增;
)时,f′(x)>0,函数f(x)单调递增; ![]() ,f′(x)<0,函数f(x)单调递减;x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增.
,f′(x)<0,函数f(x)单调递减;x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增.
综上可得:当a=0时,当x>1时,函数f(x)单调递减;当x<1时,函数f(x)单调递增.
当a= ![]() 时,函数f(x)在R上单调递增;
时,函数f(x)在R上单调递增;
当 ![]() 时,x∈(﹣∞,1)时,函数f(x)单调递增;
时,x∈(﹣∞,1)时,函数f(x)单调递增; ![]() ,函数f(x)单调递减;
,函数f(x)单调递减; ![]() ,函数f(x)单调递增.
,函数f(x)单调递增.
当a ![]() 时,x∈(﹣∞,
时,x∈(﹣∞, ![]() )时,函数f(x)单调递增;
)时,函数f(x)单调递增; ![]() ,函数f(x)单调递减;x∈(1,+∞)时,函数f(x)单调递增.
,函数f(x)单调递减;x∈(1,+∞)时,函数f(x)单调递增.
(2)解:当a=1时,函数f(x)在(0,1)上单调递减;在(1,2)上单调递增.
对任意x1∈(0,2),都有f(x1)≥f(1)=e.
又对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),
∴e≥g(x2),即x2∈(1,2)时有解,
g(x2)= ![]() ,∴存在x2∈(1,2),使得
,∴存在x2∈(1,2),使得 ![]() ≤e,即存在x2∈(1,2),使得
≤e,即存在x2∈(1,2),使得 ![]() .
.
令h(x)= ![]() ,x∈(1,2),h′(x)=
,x∈(1,2),h′(x)= ![]() ,
,
令h′(x)=0,解得x= ![]() ,
,
当x∈ ![]() 时,h′(x)>0,函数h(x)单调递增;当x∈
时,h′(x)>0,函数h(x)单调递增;当x∈ ![]() 时,h′(x)<0,函数h(x)单调递减.
时,h′(x)<0,函数h(x)单调递减.
∴当x= ![]() 时,h(x)的最大值为
时,h(x)的最大值为 ![]() =1,
=1,
综上可得:实数b的取值范围是(﹣∞,1].
【解析】(1)f′(x)=(ax2﹣x﹣a+1)ex=(ax+a﹣1)(x﹣1)ex , 对a分类讨论:当a=0时,f′(x)=﹣(x﹣1)ex , 即可得出单调性;当a>0时,f′(x)=a ![]() (x﹣1)ex , 令
(x﹣1)ex , 令 ![]() =1,解得a=
=1,解得a= ![]() .当a=
.当a= ![]() 时,当
时,当 ![]() 时,当a
时,当a ![]() 时,比较
时,比较 ![]() 与1的大小关系即可得出单调性;(2)当a=1时,函数f(x)在(0,1)上单调递减;在(1,2)上单调递增.对任意x1∈(0,2),都有f(x1)≥f(1)=e.又对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),e≥g(x2),即x2∈(1,2)时有解,g(x2)=
与1的大小关系即可得出单调性;(2)当a=1时,函数f(x)在(0,1)上单调递减;在(1,2)上单调递增.对任意x1∈(0,2),都有f(x1)≥f(1)=e.又对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),e≥g(x2),即x2∈(1,2)时有解,g(x2)= ![]() ,即存在x2∈(1,2),使得
,即存在x2∈(1,2),使得 ![]() .令h(x)=
.令h(x)= ![]() ,利用导数研究其单调性极值与最值即可得出.
,利用导数研究其单调性极值与最值即可得出.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)当x>0时, ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)试证明:(1+12)(1+23)(1+34)…(1+n(n+1))>e2n﹣3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax+b(a,b∈R)在x=ln2处的切线方程为y=x﹣2ln2. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若k为差数,当x>0时,(k﹣x)f'(x)<x+1恒成立,求k的最大值(其中f'(x)为f(x)的导函数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用 ![]() (单位:元)关于月用电量
(单位:元)关于月用电量 ![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占80%,求 ![]() 的值;
的值;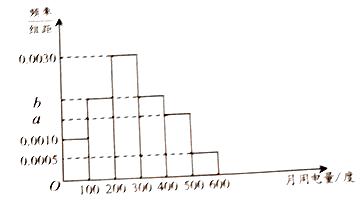
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sinxcosx﹣sin2(x﹣ ![]() ). (Ⅰ)求函数f(x)的最小正周期;
). (Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x﹣ ![]() )在[0,
)在[0, ![]() ]上的最大值与最小值.
]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在三棱柱ABC﹣A1B1C1中,B1B⊥平面ABC,∠ABC=90°,B1B=AB=2BC=4,D、E分别是B1C1 , A1A的中点. 
(1)求证:A1D∥平面B1CE;
(2)设M是的中点,N在棱AB上,且BN=1,P是棱AC上的动点,直线NP与平面MNC所成角为θ,试问:θ的正弦值存在最大值吗?若存在,请求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】)已知函数f(x)=lnx﹣2ax,a∈R.
(1)若函数y=f(x)存在与直线2x﹣y=0平行的切线,求实数a的取值范围;
(2)设g(x)=f(x)+ ![]() ,若g(x)有极大值点x1 , 求证:
,若g(x)有极大值点x1 , 求证: ![]() >a.
>a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为各项不相等的等差数列an的前n 项和,已知a3a8=3a11 , S3=9.
(1)求数列{an}的通项公式;
(2)若bn= ![]() ,数列{bn}的前n 项和为Tn , 求
,数列{bn}的前n 项和为Tn , 求 ![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com