
【题目】)已知函数f(x)=lnx﹣2ax,a∈R.
(1)若函数y=f(x)存在与直线2x﹣y=0平行的切线,求实数a的取值范围;
(2)设g(x)=f(x)+ ![]() ,若g(x)有极大值点x1 , 求证:
,若g(x)有极大值点x1 , 求证: ![]() >a.
>a.
【答案】
(1)解:因为f′(x)= ![]() ﹣2a,x>0,
﹣2a,x>0,
因为函数y=f(x)存在与直线2x﹣y=0平行的切线,
所以f′(x)=2在(0,+∞)上有解,
即 ![]() ﹣2a=2在(0,+∞)上有解,也即2+2a=
﹣2a=2在(0,+∞)上有解,也即2+2a= ![]() 在(0,+∞)上有解,
在(0,+∞)上有解,
所以2+2a>0,得a>﹣1,
故所求实数a的取值范围是(﹣1,+∞);
(2)解:证明:因为g(x)=f(x)+ ![]() x2=
x2= ![]() x2+lnx﹣2ax,
x2+lnx﹣2ax,
因为g′(x)= ![]() ,
,
①当﹣1≤a≤1时,g(x)单调递增无极值点,不符合题意,
②当a>1或a<﹣1时,令g′(x)=0,设x2﹣2ax+1=0的两根为x1和x2,
因为x1为函数g(x)的极大值点,所以0<x1<x2,
又x1x2=1,x1+x2=2a>0,所以a>1,0<x1<1,
所以g′(x1)= ![]() ﹣2ax1+
﹣2ax1+ ![]() =0,则a=
=0,则a= ![]() ,
,
要证明 ![]() +
+ ![]() >a,只需要证明x1lnx1+1>a
>a,只需要证明x1lnx1+1>a ![]() ,
,
因为x1lnx1+1﹣a ![]() =x1lnx1﹣
=x1lnx1﹣ ![]() +1=﹣
+1=﹣ ![]() ﹣
﹣ ![]() x1+x1lnx1+1,0<x1<1,
x1+x1lnx1+1,0<x1<1,
令h(x)=﹣ ![]() ﹣
﹣ ![]() x+xlnx+1,x∈(0,1),
x+xlnx+1,x∈(0,1),
所以h′(x)=﹣ ![]() x2﹣
x2﹣ ![]() +lnx,记P(x)=﹣
+lnx,记P(x)=﹣ ![]() ﹣
﹣ ![]() +lnx,x∈(0,1),
+lnx,x∈(0,1),
则P′(x)=﹣3x+ ![]() =
= ![]() ,
,
当0<x< ![]() 时,p′(x)>0,当
时,p′(x)>0,当 ![]() <x<1时,p′(x)<0,
<x<1时,p′(x)<0,
所以p(x)max=p( ![]() )=﹣1+ln
)=﹣1+ln ![]() <0,所以h′(x)<0,
<0,所以h′(x)<0,
所以h(x)在(0,1)上单调递减,所以h(x)>h(1)=0,原题得证.
【解析】(1)求出函数的导数,问题转化为2+2a= ![]() 在(0,+∞)上有解,求出a的范围即可;(2)求出g(x)的解析式,通过讨论a的范围,问题转化为证明x1lnx1+1>a
在(0,+∞)上有解,求出a的范围即可;(2)求出g(x)的解析式,通过讨论a的范围,问题转化为证明x1lnx1+1>a ![]() ,令h(x)=﹣
,令h(x)=﹣ ![]() ﹣
﹣ ![]() x+xlnx+1,x∈(0,1),根据函数的单调性证明即可.
x+xlnx+1,x∈(0,1),根据函数的单调性证明即可.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,平面PAC⊥底面ABCD,BC=CD= ![]() AC=2,∠ACB=∠ACD=
AC=2,∠ACB=∠ACD= ![]() .
. 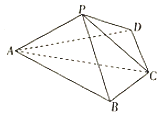
(1)证明:AP⊥BD;
(2)若AP= ![]() ,AP与BC所成角的余弦值为
,AP与BC所成角的余弦值为 ![]() ,求二面角A﹣BP﹣C的余弦值..
,求二面角A﹣BP﹣C的余弦值..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=[ax2﹣(2a+1)x+a+2]ex(a∈R).
(1)当a≥0时,讨论函数f(x)的单调性;
(2)设g(x)= ![]() ,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)若存在x0∈[ ![]() ,e](e是自然对数的底数,e=2.71828…),使不等式2f(x0)≥g(x0)成立,求实数a的取值范围.
,e](e是自然对数的底数,e=2.71828…),使不等式2f(x0)≥g(x0)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)的函数f(x)的导函数是f'(x),且x4f'(x)+3x3f(x)=ex , ![]() ,则x>0时,f(x)( )
,则x>0时,f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既无极大值,又无极小值
D.既有极大值,又有极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣2|x﹣1|. (Ⅰ)求不等式f(x)≥﹣2的解集M;
(Ⅱ)对任意x∈[a,+∞),都有f(x)≤x﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,1)与Q关于原点O对称,直线PM,QM相交于点M,且它们的斜率之积是﹣ ![]() (Ⅰ)求点M的轨迹C的方程;
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)过P作直线l交轨迹C于另一点A,求DPAO的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
A.21
B.20
C.19
D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com