
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可;
(Ⅱ)$|\frac{g(x+1)}{x}-1|<m?ln(x+1)+(m-1)x>0$,设φ(x)=ln(x+1)+(m-1)x,m>0,x>0,根据函数的单调性判断即可;
(Ⅲ)先得到lnxλ+lna1-λ≤ln[λx+(1-λ)a]令λ1=λ,λ2=1-λ,a1=x,a2=a,代入整理即可证出结论.
解答 解:(I)${f^'}(x)=\frac{{λ(1-λ)({x-a})}}{{[λx+({1-λ})a]x}}$,
∵a>0,1-λ>0,λ>0,x>0,
∴当x>a时,f′(x)>0;0<x<a时,f′(x)<0,
∴f(x)在(0,a)上单调递减,在(a,+∞)上单调递增,
∴f(x)有最小值f(a)=(1-λ)lna,没有最大值;
(II)对?m>0,?x0>0使得$|\frac{{g({x_0}+1)}}{x_0}-1|<m$成立,其理由如下:
令h(x)=ln(x+1)-x,则h′(x)≤0,
所以h(x)在[0,+∞)单调递减,
于是可得当x>0时,ln(x+1)-x<0,$\frac{{ln({x+1})}}{x}-1<0$,
故$|\frac{g(x+1)}{x}-1|<m?ln(x+1)+(m-1)x>0$,
设φ(x)=ln(x+1)+(m-1)x,m>0,x>0,
则${φ^'}(x)=\frac{1}{x+1}+m-1=\frac{{({m-1})x+m}}{x+1}$,
当m≥1时,φ′(x)>0,φ(x)在(0,+∞)上单调递增,
∴对于?x0>0均有φ(x0)>φ(0)=0恒成立,
当0<m<1时,由φ′(x)>0可得$0<x<\frac{m}{1-m}$,由φ′(x)<0可得$x>\frac{m}{1-m}$,
于是φ(x)在$(0,\frac{m}{1-m})$是增函数,在$(\frac{m}{1-m},+∞)$是减函数,
∴对于$?{x_0}∈(0,\frac{m}{1-m})$均有φ(x0)>φ(0)=0恒成立,
综上,对于任意的正数m,都存在正数x0满足条件;
证明:(III)由(I)知,对?x>0,a>0,0<λ<1时,
都有ln[λx+(1-λ)a]-λlnx≥(1-λ)lna
即lnxλ+lna1-λ≤ln[λx+(1-λ)a]
令λ1=λ,λ2=1-λ,a1=x,a2=a,
则$ln({{a_1}^{λ_1}{a_2}^{λ_2}})≤ln({{a_1}{λ_1}+{a_2}{λ_2}})$,
∵y=lnx在(0,+∞)上是增函数,
∴${a_1}^{λ_1}{a_2}^{λ_2}≤{λ_1}{a_1}+{λ_2}{a_2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.


科目:高中数学 来源: 题型:填空题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
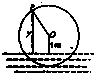 如图为一半径是4米的水轮,水轮圆心O距离水面1米,已知水轮每分钟旋转5圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+1,则( )
如图为一半径是4米的水轮,水轮圆心O距离水面1米,已知水轮每分钟旋转5圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+1,则( )| A. | $ω=\frac{π}{6},A=4$ | B. | $ω=\frac{2π}{15},A=3$ | C. | $ω=\frac{π}{6},A=5$ | D. | $ω=\frac{2π}{15},A=4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 组距 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com