
分析 (1)利用绝对值的几何意义,分类讨论解不等式f(x)≤3;
(2)由题意,m=0时,函数f(x)=|x+m|+|2x+1|的图象与直线y=3围成的多边形面积取得最大值.
解答 解:(1)当m=-1时,不等式f(x)≤3,可化为|x-1|+|2x+1|≤3,
x$≤-\frac{1}{2}$时,-x+1-2x-1≤3,∴x≥-1,∴-1≤x$≤-\frac{1}{2}$;
-$\frac{1}{2}<x<1$时,-x+1+2x+1≤3,∴x≤1,∴-$\frac{1}{2}<x<1$;
x≥1时,x-1+2x+1≤3,∴x≤1,∴x=1;
综上所述,-1≤x≤1;
(2)由题意,m=0时,函数f(x)=|x+m|+|2x+1|的图象与直线y=3围成的多边形面积取得最大值.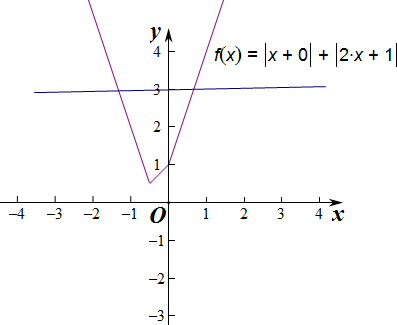
图象最低点的坐标是(-$\frac{1}{2}$,$\frac{1}{2}$),f(x)=1时,x=0或-$\frac{2}{3}$,f(x)=3时,x=-$\frac{4}{3}$或$\frac{2}{3}$,
∴函数f(x)=|x+m|+|2x+1|的图象与直线y=3围成的多边形面积的最大值为$\frac{\frac{2}{3}+2}{2}×2+\frac{1}{2}×\frac{2}{3}×\frac{1}{2}$=$\frac{17}{6}$.
点评 本题考查绝对值不等式,考查数形结合、分类讨论的数学思想,正确分类讨论是关键.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e-1-(1-ln2)e${\;}^{-\frac{1}{2}}$ | B. | ln$\frac{e}{2}$-e-1 | C. | ln2-e-1 | D. | (1-ln2)e${\;}^{-\frac{1}{2}}$-e-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥-$\frac{1}{2}$ | B. | a>0 | C. | -$\frac{1}{2}$<a<0 | D. | -$\frac{1}{2}$<a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com