【题目】如图正方体的棱长为1，线段
上有两个动点
且
，则下列结论错误的是（ ）
A. 
与
所成角为
B. 三棱锥
的体积为定值
C. 
平面
D. 二面角
是定值
【答案】A
【解析】
利用线面平行和线面垂直的判定定理和棱锥的体积公式以及二面角的定义对选项进行逐个判断即可得到答案.
选项A，AC⊥BD，AC⊥BB1，且BD 
AC⊥面DD1B1B，即得AC⊥BE，此命题错误；
选项B, 由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD1B1B距离是定值，故三棱锥A﹣BEF的体积为定值，此命题正确；
选项C，由正方体ABCD﹣A1B1C1D1的两个底面平行，EF在其一面上且EF与平面ABCD无公共点，故EF∥平面ABCD，此命题正确；
选项D，由于E、F为线段B1D1上有两个动点，故二面角A﹣EF﹣B的平面角大小始终是二面角A﹣B1D1﹣B的平面角大小，为定值，故正确；
故选：A.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图，圆形纸片的圆心为O，半径为5cm，该纸片上的正六边形ABCDEF的中心为O，G、H、M、N、P、Q为圆O上的点，△GAB，△HBC，△MCD，△NDE，△PEF，△QAF分别是以AB，BC，CD，DE，EF，FA为底边的等腰三角形，沿虚线剪开后，分别以AB，BC，CD，DE，EF，FA为折痕折起△GAB，△HBC，△MCD，△NDE，△PEF，△QAF，使得G、H、M、N、P、Q重合，得到六棱锥．当正六边形ABCDEF的边长变化时，所得六棱锥体积(单位：cm3)的最大值为（ ）
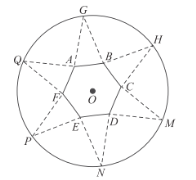
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】疫情期间，有一批货物需要用汽车从城市甲运至城市乙，已知从城市甲到城市乙只有两条公路，且通过这两条公路所用的时间互不影响.据调查统计，通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表：
所用时间 | 10 | 11 | 12 | 13 |
通过公路1的频数 | 20 | 40 | 20 | 20 |
通过公路2的频数 | 10 | 40 | 40 | 10 |
（1）为进行某项研究，从所用时间为12的60辆汽车中随机抽取6辆，若用分层随机抽样的方法抽取，求从通过公路1和公路2的汽车中各抽取几辆：
（2）若从（1)的条件下抽取的6辆汽车中，再任意抽取2辆汽车，求这2辆汽车至少有1辆通过公路1的概率；
（3）假设汽车A只能在约定时间的前11h出发，汽车B只能在约定时间的前12h出发.为了尽最大可能在各自允许的时间内将货物从城市甲运到城市乙，汽车A和汽车B应如何选择各自的道路？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若
，求曲线
在点
处的切线方程；
（2）若函数
在其定义域内为增函数，求
的取值范围；
（3）在（2）的条件下，设函数
，若在
上至少存在一点
，使得
成立，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(文)(2017·衡水二模)某商场在元旦举行购物抽奖促销活动，规定顾客从装有编号0,1,2,3,4的五个相同小球的抽奖箱中一次任意摸出两个小球，若取出的两个小球的编号之和等于7则中一等奖，等于6或5则中二等奖，等于4则中三等奖，其余结果为不中奖.
(1)求中二等奖的概率．
(2)求不中奖的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若
在
处有极值，问是否存在实数m，使得不等式
对任意
及
恒成立？若存在，求出m的取值范围；若不存在，请说明理由.
；
（2）若
，设
.
①求证：当
时，
；
②设
，求证：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直三棱柱ABC-A1B1C1中，底面△ABC是直角三角形，AC=BC=AA1=2，D为侧棱AA1的中点．
（1）求异面直线DC1，B1C所成角的余弦值；
（2）求二面角B1-DC-C1的平面角的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
