
分析 设直线PA:y=kx+1,代入椭圆方程可得A的坐标,由直线PB的方程为y=$\frac{2}{3k}$x+1,可得B的坐标,运用点到直线的距离公式和三角形的面积公式,可得S关于k的式子,运用基本不等式,即可求得最大值.
解答 解:设直线PA:y=kx+1,代入椭圆方程可得,
(1+3k2)x2+6kx=0,
解得x=0或-$\frac{6k}{1+3{k}^{2}}$,
可得A(-$\frac{6k}{1+3{k}^{2}}$,$\frac{1-3{k}^{2}}{1+3{k}^{2}}$),
由斜率kPA•kPB=$\frac{2}{3}$,
直线PB的方程为y=$\frac{2}{3k}$x+1,
代入椭圆方程,可得交点B为($\frac{-12k}{4+3{k}^{2}}$,$\frac{3{k}^{2}-4}{3{k}^{2}+4}$),
则△PAB的面积为S=$\frac{1}{2}$|PA|•d(d为B到直线PA的距离)
=$\frac{1}{2}$$\sqrt{\frac{36{k}^{2}}{(1+3{k}^{2})^{2}}+\frac{36{k}^{4}}{(1+3{k}^{2})^{2}}}$•$\frac{|k•\frac{-12k}{3{k}^{2}+4}+1-\frac{3{k}^{2}-4}{3{k}^{2}+4}|}{\sqrt{1+{k}^{2}}}$
=$\frac{12|2k-3{k}^{3}|}{(3{k}^{2}+1)(3{k}^{2}+4)}$,
可令k>0,上式分子分母同除以k2,
可得S=$\frac{12|3k-\frac{2}{k}|}{9{k}^{2}+\frac{4}{{k}^{2}}+15}$,
再令|3k-$\frac{2}{k}$|=t,
即有S=$\frac{12t}{{t}^{2}+27}$=$\frac{12}{t+\frac{27}{t}}$≤$\frac{12}{2\sqrt{27}}$=$\frac{2\sqrt{3}}{3}$.
当且仅当t=$\frac{27}{t}$即t=3$\sqrt{3}$,可得k=$\frac{3\sqrt{3}+\sqrt{51}}{6}$,
△PAB面积取得最大值$\frac{2\sqrt{3}}{3}$.
点评 本题考查椭圆的方程和性质,主要考查直线方程和椭圆方程求交点,同时考查三角形面积公式和点到直线的距离和基本不等式的运用,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
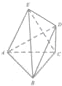 已知AC=BC=$\sqrt{2}$,CD=$\frac{\sqrt{3}}{2}$,AB=BE=EA=2,CD⊥面ABC,面ABE⊥面ABC.
已知AC=BC=$\sqrt{2}$,CD=$\frac{\sqrt{3}}{2}$,AB=BE=EA=2,CD⊥面ABC,面ABE⊥面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一个顶点为A(0,1),直线l:y=-x+2恰好与椭圆相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一个顶点为A(0,1),直线l:y=-x+2恰好与椭圆相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,四边形ABCD为菱形,∠ABC=60°,EC⊥面ABCD,FA⊥面ABCD,G为BF的中点,若EG⊥面ABF,AB=2.
如图,在多面体ABCDEF中,四边形ABCD为菱形,∠ABC=60°,EC⊥面ABCD,FA⊥面ABCD,G为BF的中点,若EG⊥面ABF,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com