Question

5．在△ABC中，点O是BC的中点，过点O的直线分别与边AB、AC所在直线交于不同的两点M、N，若向量$\overrightarrow{AB}=m\overrightarrow{AM}$，$\overrightarrow{AC}=n\overrightarrow{AN}（m，n∈R）$，则mn的最大值为（　　）

• A． $\frac{1}{4}$
• B． $\frac{1}{2}$
• C． 1
• D． 2

Answer 1

分析 延长AO至A'使AO=A'O，延长A'C交MN 于M'，利用O是BC的中点，得到三角形全等和相似，利用相似比和线段的关系列出等式，再把条件代入求出m+n的值，再利用基本不等式求出mn的最大值．

解答 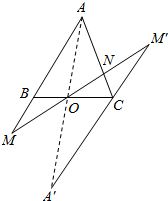解：延长AO至A′使AO=A′O，延长A′C交MN 于M′，如图所示：
则△OBM≌△OCM′，∴BM=CM′，
∵△NAM∽△NCM′，
∴$\frac{NC}{AN}$=$\frac{CM′}{AM}$，即$\frac{AN-AC}{AN}$=$\frac{AB-AM}{AM}$，
又∵$\overrightarrow{AB}=m\overrightarrow{AM}$，$\overrightarrow{AC}=n\overrightarrow{AN}（m，n∈R）$，
∴|$\overrightarrow{AB}$|=m|$\overrightarrow{AM}$|，|$\overrightarrow{AC}$|=n|$\overrightarrow{AN}$|，
代入上式得，n-1=1-m，则m+n=2；
∴m+n=2≥2$\sqrt{mn}$，即mn≤1；
∴mn的最大值为1．
故选：C．

点评 本题考查了向量在几何中的应用以及基本不等式的应用问题，也考查了数形结合思想，是中档题目．