
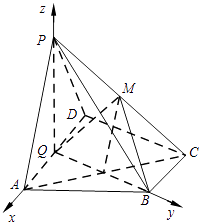
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= ![]() AD=1,CD=
AD=1,CD= ![]() .
. 
(1)求证:平面PQB⊥平面PAD;
(2)若M为棱PC的中点,求异面直线AP与BM所成角的余弦值;
(3)若二面角M﹣BQ﹣C大小为30°,求QM的长.
【答案】
(1)解:∵AD∥BC,BC= ![]() AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ
又∵∠ADC=90°,∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.∵BQ平面PQB,
∴平面PQB⊥平面PAD.
(2)解:∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则Q(0,0,0),A(1,0,0), ![]() ,
, ![]() ,C(﹣1,
,C(﹣1, ![]() ,0)
,0)
∵M是PC中点,∴ ![]() ,
,
∴ ![]()
设异面直线AP与BM所成角为θ
则cosθ= 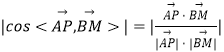 =
= ![]() ,
,
∴异面直线AP与BM所成角的余弦值为 ![]() ;
;
(3)解:由(2)知平面BQC的法向量为 ![]() ,
,
由 ![]() ,且0≤λ≤1,得
,且0≤λ≤1,得 ![]() ,
,
又 ![]() ,∴平面MBQ法向量为
,∴平面MBQ法向量为 ![]() .
.
∵二面角M﹣BQ﹣C为30°,∴ 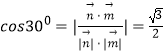 ,
,
∴ ![]() .∴|QM|=
.∴|QM|= ![]()
【解析】(1)由题意易证QB⊥AD,由面面垂直的性质可得BQ⊥平面PAD,可得结论;(2)易证PQ⊥平面ABCD,以Q为原点建立空间直角坐标系,则可得相关点的坐标,可得向量 ![]() 和
和 ![]() 的坐标,可得夹角的余弦值,由反三角函数可得答案;(3)可得平面BQC的法向量为
的坐标,可得夹角的余弦值,由反三角函数可得答案;(3)可得平面BQC的法向量为 ![]() ,又可求得平面MBQ法向量为
,又可求得平面MBQ法向量为 ![]() ,结合题意可得λ的方程,解方程可得λ,可得所求.
,结合题意可得λ的方程,解方程可得λ,可得所求.
【考点精析】本题主要考查了异面直线及其所成的角和平面与平面垂直的判定的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数
B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数
D.偶函数,且在(0,1)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】备受瞩目的巴西世界杯正在如火如荼的进行,为确保总决赛的顺利进行,组委会决定在位于里约热内卢的马拉卡纳体育场外临时围建一个矩形观众候场区,总面积为72m2(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为2m的入口.现已知铁栏杆的租用费用为100元/m.设该矩形区域的长为x(单位:m),租用铁栏杆的总费用为y(单位:元) 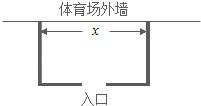
(1)将y表示为x的函数;
(2)试确定x,使得租用此区域所用铁栏杆所需费用最小,并求出最小最小费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F. 
(1)判断BE是否平分∠ABC,并说明理由;
(2)若AE=6,BE=8,求EF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足下面条件的函数y=f(x)为“ξ函数”:存在一条与函数y=f(x)的图象有两个不同交点(设为P(x1 , y1)Q(x2 , y2))的直线,y=(x)在x= ![]() 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数:
①y= ![]() ②y=x2(x>0)③y=
②y=x2(x>0)③y= ![]() ④y=lnx,
④y=lnx,
其中为“ξ函数”的是(将所有你认为正确的序号填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)的图形是圆.
(1)求t的取值范围;
(2)求圆的面积取最大值时t的值;
(3)若点P(3,4t2)恒在所给圆内,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

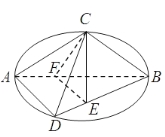
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com