
°ĺŐ‚ńŅ°ŅĪł ‹÷űńŅĶńįÕőų ņĹÁĪ≠’ż‘ŕ»ÁĽū»Á›ĪĶńĹÝ––£¨ő™»∑Ī£◊‹ĺŲ»ŁĶńň≥ņŻĹÝ––£¨◊ťőĮĽŠĺŲ∂®‘ŕőĽ”ŕņÔ‘ľ»»ńନĶń¬Ūņ≠Ņ®ń…ŐŚ”ż≥°Õ‚ŃŔ ĪőßĹ®“ĽłŲĺō–őĻŘ÷ŕļÚ≥°«Ý£¨◊‹√śĽżő™72m2£®»ÁÕľňý ĺ£©£ģ“™«ůĺō–ő≥°ĶōĶń“Ľ√śņŻ”√ŐŚ”ż≥°ĶńÕ‚«Ĺ£¨∆š”ŗ»ż√ś”√Őķņłłňőߣ¨≤Ę«““™‘ŕŐŚ”żĻ›Õ‚«Ĺ∂‘√śŃŰ“ĽłŲ≥§∂»ő™2mĶń»ŽŅŕ£ģŌ÷“—÷™ŐķņłłňĶń◊‚”√∑—”√ő™100‘™/m£ģ…Ťł√ĺō–ő«Ý”ÚĶń≥§ő™x£®Ķ•őĽ£ļm£©£¨◊‚”√ŐķņłłňĶń◊‹∑—”√ő™y£®Ķ•őĽ£ļ‘™£© 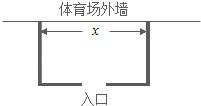
£®1£©ĹęyĪŪ ĺő™xĶńļĮ ż£Ľ
£®2£© ‘»∑∂®x£¨ ĻĶ√◊‚”√īň«Ý”Úňý”√Őķņłłňňý–Ť∑—”√◊Ó–°£¨≤Ę«ů≥Ų◊Ó–°◊Ó–°∑—”√£ģ
°ĺīūįł°Ņ
£®1£©Ĺ‚£ļ“ņŐ‚“‚”–£ļy=100£® ![]() +x©Ā2£©£¨∆š÷–x£ĺ2£Ľ
+x©Ā2£©£¨∆š÷–x£ĺ2£Ľ
£®2£©Ĺ‚£ļ”…ĺý÷Ķ≤ĽĶ» ĹŅ…Ķ√£ļy=100£® ![]() +x©Ā2£©=100£®
+x©Ā2£©=100£® ![]() +x©Ā2£©°›100£®2
+x©Ā2£©°›100£®2 ![]() ©Ā2£©=2200£¨
©Ā2£©=2200£¨
ĶĪ«“ĹŲĶĪ ![]() =x£¨ľīx=12 Ī»°°į=°Ī
=x£¨ľīx=12 Ī»°°į=°Ī
◊Ř…Ō£ļĶĪx=12 Ī£¨◊‚”√īň«Ý”Úňý”√Őķņłłňňý–Ť∑—”√◊Ó–°£¨◊Ó–°∑—”√ő™2200‘™
°ĺĹ‚őŲ°Ņ£®1£©łý囓™«ůĺō–ő≥°ĶōĶń“Ľ√śņŻ”√ŐŚ”ż≥°ĶńÕ‚«Ĺ£¨∆š”ŗ»ż√ś”√Őķņłłňőߣ¨≤Ę«““™‘ŕŐŚ”żĻ›Õ‚«Ĺ∂‘√śŃŰ“ĽłŲ≥§∂»ő™2mĶń»ŽŅŕ£ģŌ÷“—÷™ŐķņłłňĶń◊‚”√∑—”√ő™100‘™/m£ģŅ…Ķ√yĪŪ ĺő™xĶńļĮ ż£Ľ£®2£©”…ĺý÷Ķ≤ĽĶ» ĹŅ…Ķ√ĹŠ¬Ř£ģ
°ĺŅľĶ„ĺęőŲ°ŅĹ‚īūīňŐ‚ĶńĻōľŁ‘ŕ”ŕņŪĹ‚ĽýĪĺ≤ĽĶ» Ĺ‘ŕ◊Ó÷Ķő Ő‚÷–Ķń”¶”√ĶńŌŗĻō÷™ ∂£¨’∆ő’”√ĽýĪĺ≤ĽĶ» Ĺ«ů◊Ó÷Ķ Ī£®Ľż∂®ļÕ◊Ó–°£¨ļÕ∂®Ľż◊Óīů£©£¨“™◊Ę“‚¬ķ◊„»żłŲŐűľĢ°į“Ľ’ż°Ę∂Ģ∂®°Ę»żŌŗĶ»°Ī£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ√ŅńÍĶńīļĹŕļů£¨ń≥ –’Ģłģ∂ľĽŠ∑Ę∂ĮĻęőŮ‘Ī≤ő”ŽĶĹ÷≤ ų¬ŐĽĮĽÓ∂Į÷–»•£ģŃ÷“ĶĻ‹ņŪ≤Ņ√Ň‘ŕ÷≤ ų«į£¨ő™ŃňĪ£÷§ ų√ÁĶń÷ ŃŅ£¨∂ľĽŠ‘ŕ÷≤ ų«į∂‘ ų√ÁĹÝ––ľž≤‚£ģŌ÷ī”ľ◊°Ę““ŃĹ÷÷ ų√Á÷–łų≥ť≤‚Ńň10÷Í ų√Á£¨ŃŅ≥ŲňŁ√«ĶńłŖ∂»»ÁŌ¬£®Ķ•őĽ£ļņŚ√◊£©£ļ
ľ◊£ļ37£¨21£¨31£¨20£¨29£¨19£¨32£¨23£¨25£¨33£Ľ
““£ļ10£¨30£¨47£¨27£¨46£¨14£¨26£¨10£¨44£¨46£ģ
£®1£©Ľ≠≥ŲŃĹ◊ť żĺ›Ķńĺ•“∂Õľ£¨≤Ęłýĺ›ĺ•“∂Õľ∂‘ľ◊°Ę““ŃĹ÷÷ ų√ÁĶńłŖ∂»◊ųĪ»ĹŌ£¨–ī≥ŲŃĹłŲÕ≥ľ∆ĹŠ¬Ř£Ľ
£®2£©…Ť≥ť≤‚Ķń10÷Íľ◊÷÷ ų√ÁłŖ∂»∆Ĺĺý÷Ķő™![]() £¨Ĺę’‚10÷Í ų√ÁĶńłŖ∂»“ņīő š»Ž£¨įī≥Ő–ÚŅÚ£®»ÁÕľ£©ĹÝ––‘ňň„£¨ő š≥ŲĶńSīů–°ő™∂ŗ…Ŕ£Ņ≤ĘňĶ√ųSĶńÕ≥ľ∆—ß“‚“Ś£ģ
£¨Ĺę’‚10÷Í ų√ÁĶńłŖ∂»“ņīő š»Ž£¨įī≥Ő–ÚŅÚ£®»ÁÕľ£©ĹÝ––‘ňň„£¨ő š≥ŲĶńSīů–°ő™∂ŗ…Ŕ£Ņ≤ĘňĶ√ųSĶńÕ≥ľ∆—ß“‚“Ś£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņįŗ…Ō”–ňńőĽÕ¨—ß…Í«ŽA£¨B£¨C»żňýīů—ßĶń◊‘÷ų’–…ķ£¨»Ű√ŅőĽÕ¨—ß÷Ľń‹…Í«Ž∆š÷–“Ľňýīů—ߣ¨«“…Í«Ž∆š÷–»őļő“Ľňýīů—ß «Ķ»Ņ…ń‹Ķń£ģ
£®1£©«ů«°”–2»ň…Í«ŽAīů—߼ÚBīů—ßĶńłŇ¬ £Ľ
£®2£©«ů…Í«ŽCīů—ßĶń»ň żXĶń∑÷≤ľŃ–”Ž ż—ß∆ŕÕŻE£®X£©£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ŌÚŃŅ ![]() =£®1£¨3cos¶Ń£©£¨
=£®1£¨3cos¶Ń£©£¨ ![]() =£®1£¨4tan¶Ń£©£¨
=£®1£¨4tan¶Ń£©£¨ ![]() £¨«“
£¨«“ ![]() =5£ģ
=5£ģ
£®1£©«ů| ![]() +
+ ![]() |£Ľ
|£Ľ
£®2£©…ŤŌÚŃŅ ![]() ”Ž
”Ž ![]() Ķńľ–Ĺ«ő™¶¬£¨«ůtan£®¶Ń+¶¬£©Ķń÷Ķ£ģ
Ķńľ–Ĺ«ő™¶¬£¨«ůtan£®¶Ń+¶¬£©Ķń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…Ťf£®x£©”Žg£®x£© «∂®“Ś‘ŕÕ¨“Ľ«Ýľš[a£¨b]…ŌĶńŃĹłŲļĮ ż£¨»ŰļĮ ży=f£®x£©©Āg£®x£©‘ŕx° [a£¨b]…Ō”–ŃĹłŲ≤ĽÕ¨ĶńŃ„Ķ„£¨‘Ú≥∆f£®x£©ļÕg£®x£©‘ŕ[a£¨b]…Ō «°įĻōŃ™ļĮ ż°Ī£¨«Ýľš[a£¨b]≥∆ő™°įĻōŃ™«Ýľš°Ī£ģ»Űf£®x£©=x2©Ā3x+4”Žg£®x£©=2x+m‘ŕ[0£¨3]…Ō «°įĻōŃ™ļĮ ż°Ī£¨‘ÚmĶń»°÷Ķ∑∂őß £ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() °£
°£
(1)»Űf(x)‘ŕ![]() …Ōő™‘ŲļĮ ż£¨«ůmĶń»°÷Ķ∑∂őߣĽ
…Ōő™‘ŲļĮ ż£¨«ůmĶń»°÷Ķ∑∂őߣĽ
(2)»Űf(x)Ķń÷Ķ”Úő™R£¨«ůmĶń»°÷Ķ∑∂őß°£
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńņ‚◊∂P©ĀABCD÷–£¨Ķ◊√śABCDő™÷ĪĹ«Ő›–ő£¨AD°őBC£¨°ŌADC=90°„£¨∆Ĺ√śPAD°ÕĶ◊√śABCD£¨Qő™ADĶń÷–Ķ„£¨M «ņ‚PC…ŌĶńĶ„£¨PA=PD=2£¨BC= ![]() AD=1£¨CD=
AD=1£¨CD= ![]() £ģ
£ģ 
£®1£©«ů÷§£ļ∆Ĺ√śPQB°Õ∆Ĺ√śPAD£Ľ
£®2£©»ŰMő™ņ‚PCĶń÷–Ķ„£¨«ů“ž√ś÷ĪŌŖAP”ŽBMňý≥…Ĺ«Ķń”ŗŌ“÷Ķ£Ľ
£®3£©»Ű∂Ģ√śĹ«M©ĀBQ©ĀCīů–°ő™30°„£¨«ůQMĶń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() .
.
£®1£©Ň–∂ŌļĮ ż![]() ‘ŕ
‘ŕ![]() ĶńĶ•Ķų–‘.£®≤Ľ–Ť“™÷§√ų£©£Ľ
ĶńĶ•Ķų–‘.£®≤Ľ–Ť“™÷§√ų£©£Ľ
£®2£©ŐĹĺŅ «∑Ůīś‘ŕ Ķ ż![]() £¨ ĻĶ√ļĮ ż
£¨ ĻĶ√ļĮ ż![]() ő™∆śļĮ ż£Ņ»Űīś‘ŕ£¨«ů≥Ų
ő™∆śļĮ ż£Ņ»Űīś‘ŕ£¨«ů≥Ų![]() Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£Ľ
Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨Ĺ‚≤ĽĶ» Ĺ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤![]() ĶńņŽ–ń¬ ő™
ĶńņŽ–ń¬ ő™![]() £¨Õ÷‘≤
£¨Õ÷‘≤![]() ļÕŇ◊őÔŌŖ
ļÕŇ◊őÔŌŖ![]() ĹĽ”ŕ
ĹĽ”ŕ![]() ŃĹĶ„£¨«“÷ĪŌŖ
ŃĹĶ„£¨«“÷ĪŌŖ![]() «°ļ√Õ®ĻżÕ÷‘≤
«°ļ√Õ®ĻżÕ÷‘≤![]() Ķń”“ĹĻĶ„
Ķń”“ĹĻĶ„![]() £ģ
£ģ
£®1£©«ůÕ÷‘≤![]() ĶńĪÍ◊ľ∑Ĺ≥Ő£Ľ
ĶńĪÍ◊ľ∑Ĺ≥Ő£Ľ
£®2£©“—÷™Õ÷‘≤![]() Ķń◊ůĹĻĶ„ő™
Ķń◊ůĹĻĶ„ő™![]() £¨◊ů°Ę”“∂•Ķ„∑÷Īūő™
£¨◊ů°Ę”“∂•Ķ„∑÷Īūő™![]() £¨ĺ≠ĻżĶ„
£¨ĺ≠ĻżĶ„![]() Ķń÷ĪŌŖ
Ķń÷ĪŌŖ![]() ”ŽÕ÷‘≤
”ŽÕ÷‘≤![]() ĹĽ”ŕ
ĹĽ”ŕ![]() ŃĹĶ„£¨ľ«
ŃĹĶ„£¨ľ«![]() ”Ž
”Ž![]() Ķń√śĽż∑÷Īūő™
Ķń√śĽż∑÷Īūő™![]() £¨«ů
£¨«ů![]() Ķń◊Óīů÷Ķ£ģ
Ķń◊Óīů÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com