
【题目】已知向量 ![]() =(1,3cosα),
=(1,3cosα), ![]() =(1,4tanα),
=(1,4tanα), ![]() ,且
,且 ![]() =5.
=5.
(1)求| ![]() +
+ ![]() |;
|;
(2)设向量 ![]() 与
与 ![]() 的夹角为β,求tan(α+β)的值.
的夹角为β,求tan(α+β)的值.
【答案】
(1)解:由 ![]() =(1,3cosα),
=(1,3cosα), ![]() =(1,4tanα),
=(1,4tanα),
则 ![]()
![]() =1+12cosαtanα=5,解得
=1+12cosαtanα=5,解得 ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,
, ![]() .
.
则 ![]() =(1,2
=(1,2 ![]() ),
), ![]() =(1,
=(1, ![]() )
)
则 ![]() =
= ![]() ,
,
即有| ![]() |=
|= ![]() =
= ![]() ;
;
(2)解:由(1)知 ![]() =(1,2
=(1,2 ![]() ),
), ![]() =(1,
=(1, ![]() ),
),
则cosβ=cos< ![]() >=
>= ![]() =
= ![]() ,
,
即有 ![]() ,所以
,所以 ![]() ,
,
所以 
【解析】(1)由向量的数量积的坐标公式化简即得sinα,由同角公式,求得cosα,tanα,得到向量m,n,再由模的公式即可得到所求的值;(2)运用向量的夹角公式,求得cosβ,进而得到sinβ,tanβ,再由两角和的正切公式,即可得到所求的值.
【考点精析】利用数量积表示两个向量的夹角和两角和与差的正切公式对题目进行判断即可得到答案,需要熟知设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则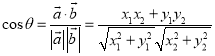 ;两角和与差的正切公式:
;两角和与差的正切公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】某校早上8:00开始上课,假设该校学生小张与小王在早上7:30~7:50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少晚5分钟到校的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF= ![]() km,FE=3km,EC=
km,FE=3km,EC= ![]() km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=
km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y= ![]() (其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分. 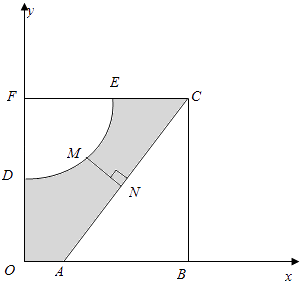
(1)求a,b,k,m的值;
(2)现准备建一座桥MN,其中M,N分别在DE,AC上,且MN⊥AC,设点M的横坐标为t.
①请写出桥MN的长l关于t的函数关系式l=f(t),并注明定义域;
②当t为何值时,l取得最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数
B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数
D.偶函数,且在(0,1)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣ax﹣3(a≠0).
(1)讨论f(x)的单调性;
(2)若f(x)+(a+1)x+4﹣e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数);
(3)求证ln(22+1)+ln(32+1)+ln(42+1)+…+ln(n2+1)<1+2lnn!(n≥2,n∈N*)(n!=1×2×3×…×n).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】备受瞩目的巴西世界杯正在如火如荼的进行,为确保总决赛的顺利进行,组委会决定在位于里约热内卢的马拉卡纳体育场外临时围建一个矩形观众候场区,总面积为72m2(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为2m的入口.现已知铁栏杆的租用费用为100元/m.设该矩形区域的长为x(单位:m),租用铁栏杆的总费用为y(单位:元) 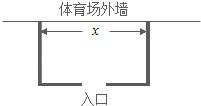
(1)将y表示为x的函数;
(2)试确定x,使得租用此区域所用铁栏杆所需费用最小,并求出最小最小费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F. 
(1)判断BE是否平分∠ABC,并说明理由;
(2)若AE=6,BE=8,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com