
【题目】如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF= ![]() km,FE=3km,EC=
km,FE=3km,EC= ![]() km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=
km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y= ![]() (其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分. 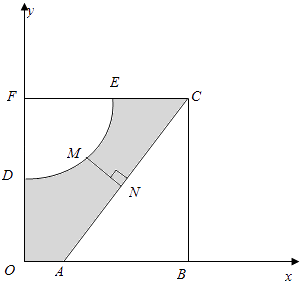
(1)求a,b,k,m的值;
(2)现准备建一座桥MN,其中M,N分别在DE,AC上,且MN⊥AC,设点M的横坐标为t.
①请写出桥MN的长l关于t的函数关系式l=f(t),并注明定义域;
②当t为何值时,l取得最小值?最小值是多少?
【答案】
(1)解:由题意得:OD=BC=4,OB=FC,
∴D(0, ![]() ),E(3,4),A(
),E(3,4),A( ![]() ,0),C(
,0),C( ![]() ,4),
,4),
把D(0, ![]() ),E(3,4)代入y=
),E(3,4)代入y= ![]()
得: 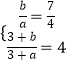 ,解得:a=﹣4,b=﹣7,
,解得:a=﹣4,b=﹣7,
把A( ![]() ,0),C(
,0),C( ![]() ,4)代入y=kx+m
,4)代入y=kx+m
得: 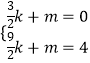 ,解得:k=
,解得:k= ![]() ,m=﹣2
,m=﹣2
(2)解:由(1)得:M点在y= ![]() 上,
上,
∴M(t, ![]() ),t∈[0,3],
),t∈[0,3],
①桥MN的长l为MN到直线y= ![]() x﹣2的距离,
x﹣2的距离,
故l=f(x)= ![]() =
= ![]() |4t+
|4t+ ![]() ﹣9|,t∈[0,3];
﹣9|,t∈[0,3];
②由①得:f(t)= ![]() |4t+
|4t+ ![]() ﹣9|=
﹣9|= ![]() |4(t﹣4)+
|4(t﹣4)+ ![]() +7|,
+7|,
而t﹣4<0, ![]() <0,
<0,
∴4(t﹣4)+ ![]() ≤﹣2
≤﹣2 ![]() =﹣12,
=﹣12,
当且仅当4(t﹣4)= ![]() 时即t=
时即t= ![]() “=”成立,
“=”成立,
∴f(t)min= ![]() |﹣12+7|=1
|﹣12+7|=1
【解析】(1)先求出D、E、A、C点的坐标,代入函数的解析式,从而求出a,b,k,m的值即可;(2)①先表示出M点的坐标,问题转化为求M到直线AC的距离即可;②由基本不等式的性质求出最小值即可.


科目:高中数学 来源: 题型:
【题目】某单位建造一间地面面积为12![]() 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度![]() 不得超过
不得超过![]() 米,房屋正面的造价为400元/
米,房屋正面的造价为400元/![]() ,房屋侧面的造价为150元/
,房屋侧面的造价为150元/![]() ,屋顶和地面的造价费用合计为5800元,如果墙高为3
,屋顶和地面的造价费用合计为5800元,如果墙高为3![]() ,且不计房屋背面的费用.
,且不计房屋背面的费用.
(1)把房屋总价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(2)当侧面的长度为多少时,总造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在每年的春节后,某市政府都会发动公务员参与到植树绿化活动中去.林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)画出两组数据的茎叶图,并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为![]() ,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数. 当x≥0时,f(x)= 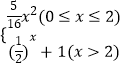 ,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是 .
,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班上有四位同学申请A,B,C三所大学的自主招生,若每位同学只能申请其中一所大学,且申请其中任何一所大学是等可能的.
(1)求恰有2人申请A大学或B大学的概率;
(2)求申请C大学的人数X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,3cosα),
=(1,3cosα), ![]() =(1,4tanα),
=(1,4tanα), ![]() ,且
,且 ![]() =5.
=5.
(1)求| ![]() +
+ ![]() |;
|;
(2)设向量 ![]() 与
与 ![]() 的夹角为β,求tan(α+β)的值.
的夹角为β,求tan(α+β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 在
在![]() 的单调性.(不需要证明);
的单调性.(不需要证明);
(2)探究是否存在实数![]() ,使得函数
,使得函数![]() 为奇函数?若存在,求出
为奇函数?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)在(2)的条件下,解不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com