
| 网络 | 月租 | 本地话费 | 长途话费 |
| 甲:联通 | 12元 | 0.3元/分钟 | 0.6元/分钟 |
| 乙:移动 | 无 | 0.5元/分钟 | 0.8元/分钟 |
分析 (1)根据条件建立函数与x的关系即可,
(2)利用作差法进行比较大小即可.
解答 解:(1)∵刘先生每月接打本地电话时间是长途电话的5倍,
∴设刘先生每月通话时间为x分钟,使用甲种入网方式所需话费的函数f(x)及使用乙种入网方式所需话费的函数g(x);
则他每月接打本地电话时间为$\frac{5}{6}$x.接打长途$\frac{1}{6}$x,
若选择甲种入网分式,则月租12元,本地话费0.3×$\frac{5}{6}$x=0.25x,长途话费0.6×$\frac{1}{6}$x=0.1x,
则f(x)=12+0.25x+0.1x=12+0.35x,(x>0).
若选择乙种入网分式,则月租0元,本地话费0.5×$\frac{5}{6}$x=$\frac{5}{12}$x,长途话费0.8×$\frac{1}{6}$x=$\frac{2}{15}$x,
则g(x)=$\frac{5}{12}$x+$\frac{2}{15}$x=0.55x,(x>0).
(2)f(x)-g(x)=12+0.35x-0.55x=12-0.2x,
当12-0.2x>0时,即x<60时,f(x)>g(x),此时应选择乙方式入网,省钱,
当12-0.2x<0时,即x>60时,f(x)<g(x),此时应选择甲方式入网,省钱,
当12-0.2x=0时,即x=60时,f(x)=g(x),此时甲乙两种方式话费一样.
点评 本题主要考查函数的应用问题,根据条件建立函数关系式是解决本题的关键.注意要进行分类讨论.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
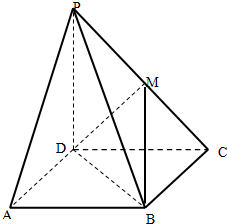 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PD⊥平面ABCD,M是PC的中点,且PD=2
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PD⊥平面ABCD,M是PC的中点,且PD=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
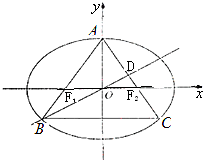 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{2}$,1),离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{2}$,1),离心率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com