
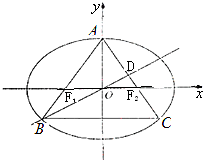
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{2}$,1),离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{2}$,1),离心率为$\frac{\sqrt{2}}{2}$.分析 (1)由e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$及a2=b2+c2,求得a2=2b2,将($\sqrt{2}$,1),代入$\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,即可求得a和b的值,求得椭圆方程,由直线AB和AC的方程,代入椭圆方程求得B和C坐标,根据点到直线的距离公式,求得点A,C到直线BO的距离之比为3:2,根据三角形的面积公式,即可求得S△ABD:S△ABC=3:5;
(2)由题意可知:设M(2,y0),P(x1,y1),直线MA1的方程为y=$\frac{{y}_{0}}{4}$x+$\frac{{y}_{0}}{2}$,代入椭圆方程,求得P坐标,根据向量数量积的坐标表示,$\overrightarrow{OP}$•$\overrightarrow{OM}$=($\frac{-2({y}_{0}^{2}-8)}{{y}_{0}^{2}+8}$,$\frac{8{y}_{0}}{{y}_{0}^{2}+8}$)(2,y0),整理可得$\overrightarrow{OP}$•$\overrightarrow{OM}$=4.
解答 解:(1)证明:由题意可知:e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,即a2=2c2,
由a2=b2+c2,则a2=2b2,
∴椭圆方程为:$\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,将($\sqrt{2}$,1),代入解得:b2=2,a2=4,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,
A(0,$\sqrt{2}$),F1(-$\sqrt{2}$,0)F2($\sqrt{2}$,0),
直线AB得斜率k=$\frac{\sqrt{2}-0}{0-(-\sqrt{2})}$=1,
直线AB的方程为:y=x+$\sqrt{2}$,代入椭圆方程得,整理得:3x2+4$\sqrt{2}$x=0,
即B(-$\frac{4\sqrt{2}}{3}$,-$\frac{\sqrt{2}}{3}$).
同理得C($\frac{4\sqrt{2}}{3}$,-$\frac{\sqrt{2}}{3}$),
直线BO为y=$\frac{1}{4}$x,
∴A到直线BO的距离为d1=$\frac{丨4\sqrt{2}丨}{\sqrt{{1}^{2}+{4}^{2}}}$=$\frac{4\sqrt{2}}{\sqrt{17}}$,
C到直线BO的距离为d2=$\frac{丨4×(-\frac{\sqrt{2}}{3})-\frac{4\sqrt{3}}{3}丨}{\sqrt{{1}^{2}+{4}^{2}}}$=$\frac{8\sqrt{3}}{3\sqrt{17}}$,
点A,C到直线BO的距离之比为3:2,
∴S△ABD:S△ABC=3:5,.
(2)证明:设M(2,y0),P(x1,y1),直线MA1的方程为y=$\frac{{y}_{0}}{4}$x+$\frac{{y}_{0}}{2}$,代入椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,整理得(1+$\frac{{y}_{0}^{2}}{8}$)x2+$\frac{{y}_{0}^{2}}{2}$x+$\frac{{y}_{0}^{2}}{2}$-4=0,
由-2x1=$\frac{4({y}_{0}^{2}-8)}{{y}_{0}^{2}+8}$,x1=$\frac{-2({y}_{0}^{2}-8)}{{y}_{0}^{2}+8}$,
从而y1=$\frac{8{y}_{0}}{{y}_{0}^{2}+8}$,
∴$\overrightarrow{OP}$•$\overrightarrow{OM}$=($\frac{-2({y}_{0}^{2}-8)}{{y}_{0}^{2}+8}$,$\frac{8{y}_{0}}{{y}_{0}^{2}+8}$)(2,y0)=$\frac{-4({y}_{0}^{2}-8)}{{y}_{0}^{2}+8}$+$\frac{{8y}_{0}^{2}}{{y}_{0}^{2}+8}$=4,
$\overrightarrow{OP}$•$\overrightarrow{OM}$为定值4.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,点到直线的位置关系,三角形面积公式,向量数量积的坐标表示,考查计算能力,属于中档题.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:选择题
| A. | 真命题、真命题 | B. | 假命题、真命题 | C. | 真命题、假命题 | D. | 假命题、假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 网络 | 月租 | 本地话费 | 长途话费 |
| 甲:联通 | 12元 | 0.3元/分钟 | 0.6元/分钟 |
| 乙:移动 | 无 | 0.5元/分钟 | 0.8元/分钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-5)∪(5,+∞) | B. | (-∞,-5)∪[5,+∞) | C. | (-∞,-5]∪[5,+∞) | D. | (-∞,-5]∪(5,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com