
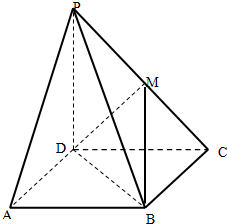
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PD⊥平面ABCD,M是PC的中点,且PD=2
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PD⊥平面ABCD,M是PC的中点,且PD=2分析 (1)根据线面平行的判定定理证明OM∥PA即可.
(2)利用线面垂直的性质,证明BC⊥平面PAD即可,
(3)根据三棱锥的体积公式进行求解.
解答 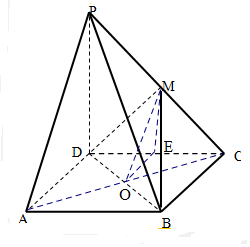 解:(1)连接AC交BD于O,连接OM,
解:(1)连接AC交BD于O,连接OM,
则OM是△PAC的中位线,
则OM∥PA,
∵OM?平面MBD,PA?平面MBD,
∴AP∥平面MBD;
(2)∵PD⊥平面ABCD,底面ABCD是边长为2的正方形,PD=2,
∴BC⊥平面PAD,
∵DM?平面平面PAD,
∴BC⊥DM,
即DM⊥BC;
(3)过M作ME⊥CD于E,
则ME⊥平面ABCD,且ME=$\frac{1}{2}$PD=1,
△BCD的面积S=$\frac{1}{2}×2×2$=2,
则三棱锥M-BCD的体积V=$\frac{1}{3}$×2×1=$\frac{2}{3}$.
点评 本题主要考查空间线面平行以及线面垂直的判断以及几何体的体积的计算,根据相应的判定定理和棱锥的体积公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | C. | $\overrightarrow a$-$\overrightarrow b$+$\overrightarrow c$ | D. | $\overrightarrow a$-$\overrightarrow b$-$\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 网络 | 月租 | 本地话费 | 长途话费 |
| 甲:联通 | 12元 | 0.3元/分钟 | 0.6元/分钟 |
| 乙:移动 | 无 | 0.5元/分钟 | 0.8元/分钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-2,-1) | C. | (-1,2) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com