
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
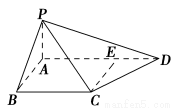
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=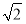 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:填空题
(2013·广东卷)给定区域D: 令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定________条不同的直线.
令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定________条不同的直线.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:解答题
已知直线l:y=x+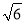 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: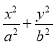 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=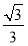 ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.
(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证:两切线的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:选择题
当直线l:y=k(x-1)+2被圆C:(x-2)2+(y-1)2=5截得的弦最短时,k的值为( ).
A.2 B. 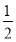 C.3 D.1
C.3 D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(解析版) 题型:选择题
在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是 ( ).
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(解析版) 题型:选择题
设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( ).
A.πa2 B. 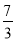 πa2 C.
πa2 C. 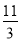 πa2 D.5πa2
πa2 D.5πa2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:填空题
设1=a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等比数列,a2、a4、a6成公差为1的等差数列,则q的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习3-2解三角形练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别是a,b,c,设平面向量e1= ,e2=
,e2= ,且e1⊥e2.
,且e1⊥e2.
(1)求cos 2A的值;
(2)若a=2,求△ABC的周长L的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习1-2算法与程序框图等练习卷(解析版) 题型:填空题
(a+x)(1+  )5的展开式中x2项的系数是15,则展开式的所有项系数的和是________.
)5的展开式中x2项的系数是15,则展开式的所有项系数的和是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com