
已知直线l:y=x+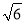 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: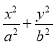 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=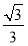 ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.
(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证:两切线的斜率之积为定值.
(1)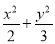 =1.(2)-1
=1.(2)-1
【解析】设椭圆的半焦距为c,
圆心O到直线l的距离d= =
=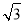 ,
,
∴b=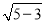 =
=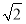 .
.
由题意得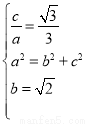 ∴a2=3,b2=2.
∴a2=3,b2=2.
∴椭圆E的方程为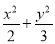 =1.
=1.
(2)证明 设点P(x0,y0),过点P的椭圆E的切线l0的方程为y-y0=k(x-x0),
联立直线l0与椭圆E的方程得
消去y得(3+2k2)x2+4k(y0-kx0)x+2(kx0-y0)2-6=0,
∴Δ=[4k(y0-kx0)]2-4(3+2k2)[2(kx0-y0)2-6]=0,
整理得:(2-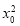 )k2+2kx0y0-(
)k2+2kx0y0-(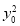 -3)=0,
-3)=0,
设满足题意的椭圆E的两条切线的斜率分别为k1,k2,则k1·k2=-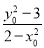 ,
,
∵点P在圆O上,∴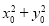 =5,
=5,
∴k1·k2=- =-1.
=-1.
∴两条切线的斜率之积为常数-1.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(解析版) 题型:选择题
将函数y=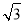 cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).
cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).
A. 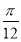 B.
B. 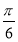 C.
C. 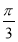 D.
D. 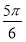
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:填空题
已知[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.2]=-2.x0是函数f(x)=ln x-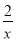 的零点,则[x0]=________.
的零点,则[x0]=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:选择题
同时满足两个条件:①定义域内是减函数;②定义域内是奇函数的函数是( ).
A.f(x)=-x|x| B.f(x)=x3
C.f(x)=sin x D.f(x)=
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:选择题
已知ξ~N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=( ).
A.0.4 B.0.3
C.0.1 D.0.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:选择题
若点O和点F分别为椭圆 的中心和左焦点,点P为椭圆上任意一点,则
的中心和左焦点,点P为椭圆上任意一点,则 的最大值( ).
的最大值( ).
A.2 B.3 C.6 D.8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:填空题
设直线3x+4y-5=0与圆C1:x2+y2=4交于A,B两点,若圆C2的圆心在线段AB上,且圆C2与圆C1相切,切点在圆C1的劣弧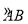 上,则圆C2的半径的最大值是________.
上,则圆C2的半径的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-1空间几何体与点等练习卷(解析版) 题型:解答题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
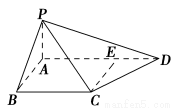
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=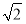 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习3-1三角函数与三角恒等变换练习卷(解析版) 题型:填空题
已知 <β<α<π,sin(α+β)=
<β<α<π,sin(α+β)= ,sin
,sin =
= ,则cos
,则cos =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com