练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若点O和点F分别为椭圆的中心和左焦点，点P为椭圆上任意一点，则的最大值(　　)．

    A．2 B．3 C．6 D．8

     

    C

    【解析】由椭圆方程得F(－1,0)，设P(x0，y0)，

    则＝(x0，y0)·(x0＋1，y0)＝＋x0＋

    ∵P为椭圆上一点，∴＋＝1.

    ∴＝＋x0＋3＝＋x0＋3＝(x0＋2)2＋2.

    ∵－2≤x0≤2.

    ∴的最大值在x0＝2时取得，且最大值等于6.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练5练习卷（解析版） 题型：解答题

    已知x＝3是函数f(x)＝aln(1＋x)＋x2－10x的一个极值点．

    (1)求a；

    (2)求函数f(x)的单调区间；

    (3)若直线y＝b与函数y＝f(x)的图象有3个交点，求b的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练2练习卷（解析版） 题型：选择题

    已知函数f(x)＝则函数f(x)的零点为 (　　)．

    A. 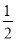，0 B．－2,0 C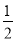． D．0

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习7-2随机变量及其分布练习卷（解析版） 题型：填空题

    将一枚均匀的硬币抛掷6次，则正面出现的次数比反面出现的次数多的概率为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习6-2椭圆、双曲线、抛物线练习卷（解析版） 题型：解答题

    已知直线l：y＝x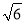＋，圆O：x2＋y2＝5，椭圆E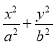：＝1(a＞b＞0)的离心率e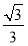＝，直线l被圆O截得的弦长与椭圆的短轴长相等．

    (1)求椭圆E的方程；

    (2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两切线的斜率之积为定值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习6-1直线与圆练习卷（解析版） 题型：解答题

    已知圆C：x2＋y2＋x－6y＋m＝0与直线l：x＋2y－3＝0.

    (1)若直线l与圆C没有公共点，求m的取值范围；

    (2)若直线l与圆C相交于P、Q两点，O为原点，且OP⊥OQ，求实数m的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习6-1直线与圆练习卷（解析版） 题型：选择题

    当直线l：y＝k(x－1)＋2被圆C：(x－2)2＋(y－1)2＝5截得的弦最短时，k的值为(　　)．

    A．2 B. 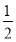C．3 D．1

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习5-1空间几何体与点等练习卷（解析版） 题型：选择题

    设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个球面上，则该球的表面积为(　　)．

    A．πa2 B. 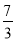πa2 C. 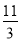πa2 D．5πa2

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习3-1三角函数与三角恒等变换练习卷（解析版） 题型：选择题

    函数y＝－2sin x的图象大致是(　　)．

     

     

    查看答案和解析>>

    同步练习册答案