
如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,
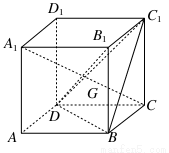
(1)求证:A1、G、C三点共线;
(2)求证:A1C⊥平面BC1D;
(3)求点C到平面BC1D的距离.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-4直线与圆、圆与圆的位置关系(解析版) 题型:填空题
已知直线l:x-y+4=0与圆C:(x-1)2+(y-1)2=2,则圆C上各点到l距离的最小值为________,最大值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:填空题
若关于x的方程|x-1|-kx=0有且只有一个正实数根,则实数k的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:解答题
如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.
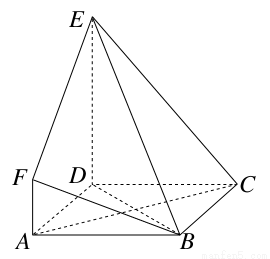
(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹为( )
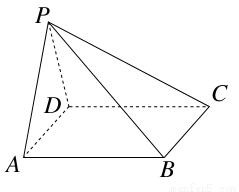
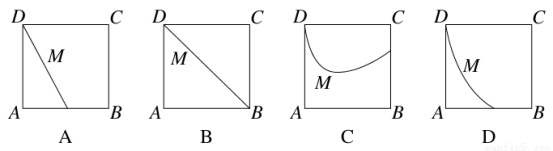
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:填空题
如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为________.
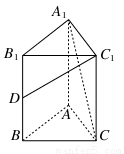
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若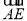 =
=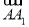 +x
+x +y
+y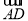 ,则x、y的值分别为( )
,则x、y的值分别为( )
A.x=1,y=1 B.x=1,y=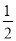
C.x=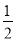 ,y=
,y=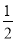 D.x=
D.x= ,y=1
,y=1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-4直线、平面平行的判定及性质(解析版) 题型:选择题
在正方体ABCD-A1B1C1D1中,点M,N分别在线段AB1,BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,其中有可能成立的个数为( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:选择题
一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )
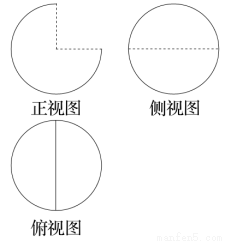
A.16π B.14π C.12π D.8π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com