
分析 (1)由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,能求出点A的直角坐标和曲线C的直角坐标方程,并得到曲线C是以(1,0)为圆心,以$\sqrt{2}$为半径的圆.
(2)设B($1+\sqrt{2}cosθ$,$\sqrt{2}sinθ$),从而线段AB的中点D(2+$\frac{\sqrt{2}}{2}cosθ$,$\frac{3}{2}+\frac{\sqrt{2}}{2}sinθ$),消去参数t,得直线l的普通方程为x-y+3=0,由此利用点到直线距离公式和三角函数性质能求出线段AB的中点D到直线l距离的最大值.
解答 解:(1)∵平面直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,点A(3$\sqrt{2}$,$\frac{π}{4}$),
∴$x=3\sqrt{2}×cos\frac{π}{4}$=3,y=3$\sqrt{2}$×$sin\frac{π}{4}$=3,
∴点A的直角坐标为A(3,3),
∵曲线C:ρ2=2ρcosθ+1,
∴曲线C的直角坐标方程为x2+y2=2x+1,即(x-1)2+y2=2,
曲线C是以(1,0)为圆心,以$\sqrt{2}$为半径的圆.
(2)∵点B是曲线C上的动点,∴设B($1+\sqrt{2}cosθ$,$\sqrt{2}sinθ$),
∴线段AB的中点D(2+$\frac{\sqrt{2}}{2}cosθ$,$\frac{3}{2}+\frac{\sqrt{2}}{2}sinθ$),
∵直线l的参数方程是$\left\{\begin{array}{l}{x=-3+t}\\{y=t}\end{array}\right.$(t是参数),
∴消去参数t,得直线l的普通方程为x-y+3=0,
∴点D(2+$\frac{\sqrt{2}}{2}cosθ$,$\frac{3}{2}+\frac{\sqrt{2}}{2}sinθ$)到直线x-y+3=0的距离:
d=$\frac{|2+\frac{\sqrt{2}}{2}cosθ-\frac{3}{2}-\frac{\sqrt{2}}{2}sinθ+3|}{\sqrt{2}}$=$\frac{|sin(θ+\frac{3π}{4})+\frac{7}{2}|}{\sqrt{2}}$,
∴当$sin(θ+\frac{3π}{4})=1$时,线段AB的中点D到直线l距离的最大值为dmax=$\frac{9\sqrt{2}}{4}$.
点评 本题考查点的直角坐标及曲线的直角坐标方程的求法,考查线段的中点到直线距离的最大值的求法,是基础题,解题时要认真审题,注意点到直线距离公式的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2+\sqrt{2}}$ | B. | $\sqrt{2+2\sqrt{2}}$ | C. | $\sqrt{1+\sqrt{2}}$ | D. | $\sqrt{1+2\sqrt{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
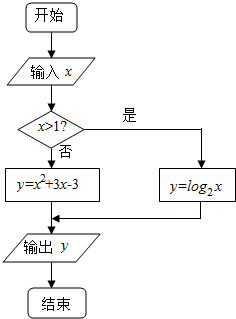
| A. | (-4,2]∪[2,+∞) | B. | [-4,1]∪[2,+∞) | C. | [-4,-2]∪{1}∪[4,+∞) | D. | (-∞,-4]∪{1}∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
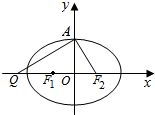 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com