练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

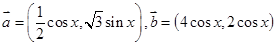    已知向量函数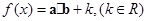
    （Ⅰ）求的单调增区间；
    （Ⅱ）若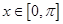时，的最大值为4，求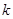的值.

    （Ⅰ）（Ⅱ）

    解析试题分析：
    …………3分
    (Ⅰ)
    所以的单调增区间为；  
    （Ⅱ）在上单调递增， 在上单调递减，在上单调递增，所以的最大值为，所以 
    考点：三角函数性质及向量的数量积运算
    点评：若则，求形如的三角函数单调区间时首先将看做一个整体在相应的单调区间内

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出，当每辆车的月租金每增加50元时，未租出的车将会增加一辆，租出的车每辆每月需维护费150元，未租出的车每辆每月需要维护费50元.
    （1）当每辆车的月租金定为3600元时，能租出多少辆车？
    （2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图所示，要用栏杆围成一个面积为50平方米的长方形花园，其中有一面靠墙不需要栏杆，其中正面栏杆造价每米200元，两个侧面栏杆每米造价50元，设正面栏杆长度为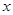米.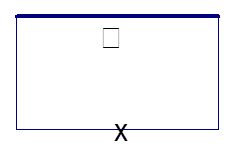

    （1）将总造价y表示为关于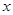的函数；
    （2）问花园如何设计，总造价最少？并求最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知，
    （1）当时，解不等式；
    （2）若，解关于的不等式。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙，已知从城市甲到城市乙只有两条公路，且通过这两条公路所用的时间互不影响。
    据调查统计，通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表：

    所用的时间（天数）
    		10
    		11
    		12
    		13
    通过公路1的频数
    		20
    		40
    		20
    		20
    通过公路2的频数
    		10
    		40
    		40
    		10
    假设汽车A只能在约定日期（某月某日）的前11天出发，汽车B只能在约定日期的前12天出发。
    （1）为了尽最大可能在各自允许的时间内将货物运往城市乙，估计汽车A和汽车B应如何选择各自的路径；
    （2）若通过公路1、公路2的“一次性费用”分别为3.2万元、1.6万元（其它费用忽略不计），此项费用由生产商承担。如果生产商恰能在约定日期当天将货物送到，则销售商一次性支付给生产商40万元，若在约定日期前送到，每提前一天销售商将多支付给生产商2万元；若在约定日期后送到，每迟到一天销售商将少支付给生产商2万元。如果汽车A、B长期按（1）所选路径运输货物，试比较哪辆汽车为生产商获得的毛利润更大。
    （注：毛利润=（销售商支付给生产商的费用）—（一次性费用））

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设为奇函数，为常数，
    （1）求的值；
    （2）证明在区间上单调递增；
    （3）若，不等式恒成立，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当居民用水超过4吨时，超过部分每吨3.00元。若某月某用户用水量为x吨，交水费为y元。
    （1）求y关于x的函数关系
    （2）若某用户某月交水费为31.2元，求该用户该月的用水量。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，.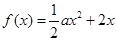
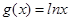    (1)设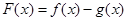函数，求函数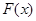的单调区间；
    (2)是否存在实数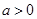，使得方程在区间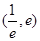内有且只有两个不相等的实数根？若存在，请求出的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某地政府鉴于某种日常食品价格增长过快，欲将这种食品价格控制在适当范围内，决定对这种食品生产厂家提供政府补贴，设这种食品的市场价格为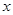元/千克，政府补贴为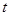元/千克，根据市场调查，当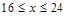时，这种食品市场日供应量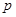万千克与市场日需量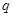万千克近似地满足关系: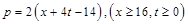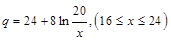，。当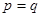市场价格称为市场平衡价格。
    （1）将政府补贴表示为市场平衡价格的函数，并求出函数的值域；
    （2）为使市场平衡价格不高于每千克20元，政府补贴至少为每千克多少元？

    查看答案和解析>>

    同步练习册答案