
 x2�ϵĵ㣬����Bn��n��bn����������y=
x2�ϵĵ㣬����Bn��n��bn����������y= x2�����߽�x���ڵ�An��an��0������Cn��cn��0����x���ϣ��ҵ�An��Bn��Cn�����Ե�BnΪ����ĵ��������Σ�
x2�����߽�x���ڵ�An��an��0������Cn��cn��0����x���ϣ��ҵ�An��Bn��Cn�����Ե�BnΪ����ĵ��������Σ�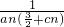 }��ǰn���ΪSn����֤��
}��ǰn���ΪSn����֤�� ��Sn��
��Sn�� ��
�� x2����y��=
x2����y��= ��y��|x=n=
��y��|x=n= ��
�� x2�����߷���Ϊ��y-
x2�����߷���Ϊ��y- =
= ��x-n����
��x-n���� ����an=
����an= ����3�֣�
����3�֣�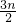 ��5�֣�
��5�֣� ����n=2��
����n=2�� =
=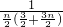 =
=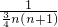 =
= ��
�� -
- ����11�֣�
����11�֣� ��1-
��1- +
+ -
- +��+
+��+ -
- ��=
��= ��1-
��1- ����
����
 ��n�����������
��n����������� ��1-
��1-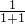 ��=
��= ��
�� ��Sn��
��Sn�� ��14�֣�
��14�֣� x2�����߷��̣���y=0���ɵ�an=
x2�����߷��̣���y=0���ɵ�an= �����ݵ�An��Bn��Cn�����Ե�BnΪ����ĵ��������Σ��ɵ�an+cn=2n���ɴ˿�������{an}��{cn}��ͨ�ʽ��
�����ݵ�An��Bn��Cn�����Ե�BnΪ����ĵ��������Σ��ɵ�an+cn=2n���ɴ˿�������{an}��{cn}��ͨ�ʽ�� =
=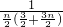 =
=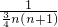 =
= ��
�� -
- �����Ӷ�����Sn=
�����Ӷ�����Sn= ��1-
��1- ����������֪
����������֪ ��Sn��
��Sn�� ��
��

 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| an |
| a1 |
| an |
| an |
| an-1 |
| an |
| 1 |
| 2 |
| a1 |
| a2 |
| an |
| a1 |
| b1 |
| b2 |
| bn |
| OBn |
| b1 |
| b2 |
| bn |
| lim |
| n���� |
| lim |
| n���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| an |
| a1 |
| an |
| 1 |
| 2 |
| an |
| a |
| a |
| a |
| a1 |
| a2 |
| an |
| a1 |
| b1 |
| b2 |
. |
| bn |
| OB |
| b1 |
| b2 |
| bn |
| lim |
| n���� |
| lim |
| n���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��߿���ѧ��һ�ָ�ϰ������9 ���ͣ�013
����{an}��a1��1��a5��13��an+2��an��2an+1������{bn}�У�b2��6��b3��3��bn+2bn��b![]() ����ֱ������ƽ���ڣ���֪����P1(a1��b1)��P2(a2��b2)��P3(a3��b3)������Pn(an��bn)����������
����ֱ������ƽ���ڣ���֪����P1(a1��b1)��P2(a2��b2)��P3(a3��b3)������Pn(an��bn)����������![]() ������P2009P2010������Ϊ
������P2009P2010������Ϊ
(3015��8[(![]() )1005��1])
)1005��1])
(3012)��8[(![]() )1005��1]
)1005��1]
(3015��8[(![]() )2010��1])
)2010��1])
(3018��8[(![]() )2010��1])
)2010��1])
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��0108 ģ���� ���ͣ���ѡ��
 ������Ϊ
������Ϊ ��1005-1]��
��1005-1]�� ��1005-1]��
��1005-1]�� ��2010-1]��
��2010-1]�� ��2010-1]��
��2010-1]���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����{an}��a1=1��a5=13��an��2��an=2an+1������{bn}�У�b2=6��b3=3��bn��2bn=b2n+1,��ֱ������ƽ���ڣ���֪����P1(a1��b1)��P2(a2��b2)��P3(a3��b3)������Pn(an��bn)������������![]()
![]() ��
��![]() ��
��![]() ������
������![]() �������� ��
�������� ��![]()
A�� B��
B��
C�� D��
D��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com