
分析 将参数方程化为普通方程,求出圆心到直线的距离,利用勾股定理求出|AB|.
解答 解:直线l:$\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),普通方程为y=$\sqrt{3}$(x-1),
曲线C1:$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$ (θ为参数),普通方程为x2+y2=1.
圆心到直线的距离d=$\frac{\sqrt{3}}{2}$,
∴|AB|=2$\sqrt{1-\frac{3}{4}}$=1.
点评 本题考查参数方程化为普通方程,考查点到直线的距离公式,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:选择题
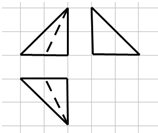 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的体积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的体积为( )| A. | 4 | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=f(x)为R上可导函数,则f'(x0)=0是x0为函数f(x)极值点的充要条件 | |
| B. | 命题“$?{x_0}∈R,{x_0}^2+{x_0}-1<0$”的否定是“?x∈R,x2+x-1>0” | |
| C. | “$φ=kπ+\frac{π}{2}(k∈Z)$”是“函数f(x)=sin(ωx+φ)是偶函数”的充要条件 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{2},4}]$ | B. | $[{2,\frac{9}{2}}]$ | C. | [-11,-1] | D. | [-3,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com