
| A. | 函数y=f(x)为R上可导函数,则f'(x0)=0是x0为函数f(x)极值点的充要条件 | |
| B. | 命题“$?{x_0}∈R,{x_0}^2+{x_0}-1<0$”的否定是“?x∈R,x2+x-1>0” | |
| C. | “$φ=kπ+\frac{π}{2}(k∈Z)$”是“函数f(x)=sin(ωx+φ)是偶函数”的充要条件 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
分析 举例说明A错误;写出命题的否定判断B;由充分必要条件的判定方法判断C;写出命题的逆命题并判断真假判断D.
解答 解:对于A,函数y=f(x)为R上可导函数,则f′(x0)=0是x0为函数f(x)极值点的比要不充分条件,如f(x)=x3,f′(x)=3x2,满足f′(0)=0,但0不是函数的极值点,故A错误;
对于B,命题“$?{x_0}∈R,{x_0}^2+{x_0}-1<0$”的否定是“?x∈R,x2+x-1≥0”,故B错误;
对于C,若$φ=kπ+\frac{π}{2}(k∈Z)$,则f(x)=sin(ωx+φ)=sin(ωx+$kπ+\frac{π}{2}$)=±cosωx,函数为偶函数,反之,若函数f(x)=sin(ωx+φ)是偶函数,
则ω×0+φ=$kπ+\frac{π}{2}$,即$φ=kπ+\frac{π}{2}(k∈Z)$,∴“$φ=kπ+\frac{π}{2}(k∈Z)$”是“函数f(x)=sin(ωx+φ)是偶函数”的充要条件,故C正确;
对于D,在△ABC中,“若A>B,则sinA>sinB”的逆命题为:“若sinA>sinB,则A>B”,由正弦定理可知:在△ABC中,a>b?A>B?sinA>sinB,
逆命题为真命题,故D错误.
故选:C.
点评 本题考查命题的真假判断与应用,考查了函数的导函数的零点与极值点的关系,考查充分必要条件的判定方法,是中档题.


科目:高中数学 来源: 题型:选择题
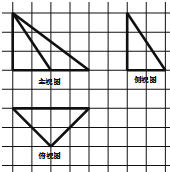 如图是某四面体ABCD水平放置时的三视图(图中网格纸的小正方形的边长为1,则四面体ABCD外接球的表面积为( )
如图是某四面体ABCD水平放置时的三视图(图中网格纸的小正方形的边长为1,则四面体ABCD外接球的表面积为( )| A. | 20π | B. | $\frac{125}{6}π$ | C. | 25π | D. | 100π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (-∞,2] | C. | [-2,+∞) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | 0 | C. | $-\frac{3}{2}$或0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com