
分析 (1)由题意可知:设椭圆方程$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),a+c=3,a-c=1,b2=a2-c2,即可求得a和b的值,求得椭圆方程;
(2)将直线方程代入椭圆方程,整理得:7x2+8mx+4(m2-3)=0,由题意可知△≥0,即可求得m的取值范围.
解答 解:(1)由题意设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由已知得:a+c=3,a-c=1,
∴a=2,c=1
∴b2=a2-c2=3,
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)将直线方程代入椭圆方程$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,
整理得:7x2+8mx+4(m2-3)=0,
由直线l:y=x+m与椭圆C有交点,
∴△≥0,即64m2-16×7×(m2-3)≥0,整理得:m2≤7,
解得:-$\sqrt{7}$≤m≤$\sqrt{7}$,
∴m的取值范围[-$\sqrt{7}$,$\sqrt{7}$].
点评 本题考查椭圆的标准方程及简单性质,考查直线与椭圆的位置关系,考查计算能力,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=f(x)为R上可导函数,则f'(x0)=0是x0为函数f(x)极值点的充要条件 | |
| B. | 命题“$?{x_0}∈R,{x_0}^2+{x_0}-1<0$”的否定是“?x∈R,x2+x-1>0” | |
| C. | “$φ=kπ+\frac{π}{2}(k∈Z)$”是“函数f(x)=sin(ωx+φ)是偶函数”的充要条件 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2 | B. | 1 | C. | b2 | D. | c2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
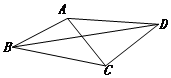 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥DC,CD=$\sqrt{3}$AC.设∠ABC=θ.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥DC,CD=$\sqrt{3}$AC.设∠ABC=θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com