
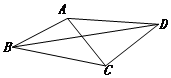
 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥DC,CD=$\sqrt{3}$AC.设∠ABC=θ.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥DC,CD=$\sqrt{3}$AC.设∠ABC=θ.分析 (1)在△ABC中,利用余弦定理可求AC,进而在△ACD中,利用勾股定理可求AD的值.
(2)设AC=x,CD=$\sqrt{3}$x,在△ABC中,利用余弦定理可求x2=4-2$\sqrt{3}$cosθ,利用正弦定理可得sin∠ACB=$\frac{sinθ}{x}$,进而利用三角函数恒等变换的应用,余弦定理可求BD=$\sqrt{15+12sin(θ-\frac{π}{3})}$,结合范围θ∈(0,π),利用正弦函数的图象和性质可求BD的最大值.
解答 (本题满分为12分)
解:(1)在△ABC中,AC2=AB2+BC2-2AB•BC•cos∠ABC,
∴AC2=1+3-2$\sqrt{3}$cos30°=1,
∴AC=1…(2分)
在△ACD中,AD2=AC2+DC2=4AC2=4,
∴AD=2.…(4分)
(2)设AC=x,CD=$\sqrt{3}$x,
在△ABC中,AC2=AB2+BC2-2AB•BC•cos∠ABC,
x2=4-2$\sqrt{3}$cosθ,…(5分)
∵$\frac{AC}{sinθ}$=$\frac{AB}{sin∠ACB}=\frac{1}{sin∠ACB}$,
∴sin∠ACB=$\frac{sinθ}{x}$.…(7分)
在△BCD中,BD=$\sqrt{(\sqrt{3})^{2}+(\sqrt{3}x)^{2}-2\sqrt{3}•(\sqrt{3}x)cos(\frac{π}{2}+∠ACB)}$=$\sqrt{3+3{x}^{2}+6xsin∠ACB}$
=$\sqrt{3+12-6\sqrt{3}cosθ+6x\frac{sinθ}{x}}$=$\sqrt{15-6\sqrt{3}cosθ+6sinθ}$=$\sqrt{15+12(\frac{1}{2}sinθ-\frac{\sqrt{3}}{2}cosθ)}$=$\sqrt{15+12sin(θ-\frac{π}{3})}$,…(10分)
∵θ∈(0,π),
∴θ-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{2π}{3}$),当θ-$\frac{π}{3}$=$\frac{π}{2}$,θ=$\frac{5π}{6}$时BD取到最大值3$\sqrt{3}$.…(12分)
点评 本题主要考查了余弦定理,勾股定理三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的综合应用,考查了计算能力和转化思想,考查了数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (-∞,2] | C. | [-2,+∞) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
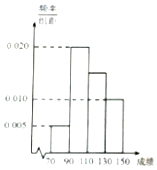 某班学生一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],若成绩大于等于90分的人数为36,则成绩在[110,130)的人数为( )
某班学生一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],若成绩大于等于90分的人数为36,则成绩在[110,130)的人数为( )| A. | 12 | B. | 9 | C. | 15 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | 0 | C. | $-\frac{3}{2}$或0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{1}{x}$? | B. | $f(x)={(\frac{1}{3})^x}$ | C. | f(x)=-x2+1 | D. | f(x)=lg|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com