
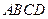 中,
中,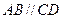 ,
,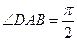 ,点
,点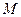 、
、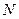 分别在
分别在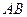 ,
,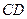 上,且
上,且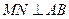 ,
,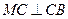 ,
,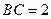 ,
,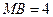 ,现将梯形
,现将梯形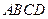 沿
沿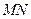 折起,使平面
折起,使平面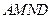 与平面
与平面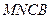 垂直(如图乙).
垂直(如图乙).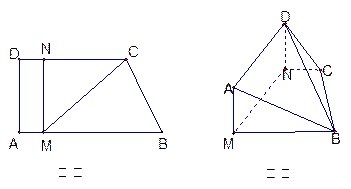
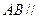 平面
平面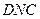 ;
;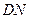 的长为何值时,
的长为何值时,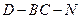 的大小为
的大小为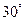 ?
?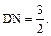
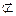 平面DNC,NC
平面DNC,NC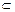 平面DNC,
平面DNC,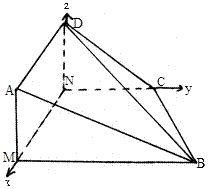
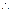 MB//平面DNC.
MB//平面DNC.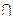 MB="M," 且MA,MB
MB="M," 且MA,MB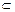 平面MAB.
平面MAB.
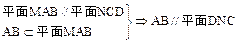 . (6分)
. (6分) 交BC延长线于H,连HN,
交BC延长线于H,连HN, 平面AMND
平面AMND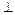 平面MNCB,DN
平面MNCB,DN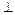 MN,
MN,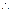 DN
DN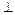 平面MBCN,从而
平面MBCN,从而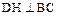 ,
,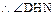 为二面角D-BC-N的平面角. (9分)
为二面角D-BC-N的平面角. (9分)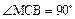 知
知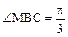 ,
, .
. 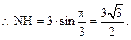 (10分)
(10分)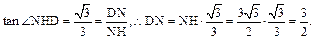 (13分)
(13分)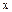 轴,
轴,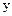 轴和
轴和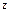 轴,建立空间直角坐标系
轴,建立空间直角坐标系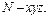 易得NC=3,MN=
易得NC=3,MN=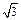 ,
,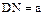 ,则
,则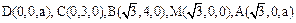 .
.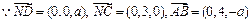 .
.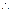
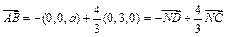 ,
, ,
,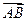 与平面
与平面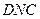 共面,又
共面,又 ,
,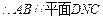 . (6分)
. (6分)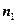
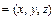 ,
,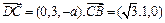
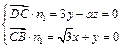 ,令
,令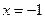 ,则
,则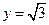 ,
,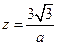
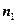
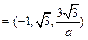 . (8分)又平面NBC的法向量
. (8分)又平面NBC的法向量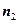
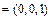 . (9分)
. (9分)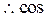
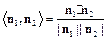
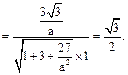
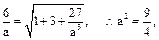 又
又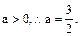 即
即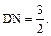 (13分)
(13分)

科目:高中数学 来源:不详 题型:解答题
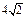 a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若
a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若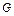 为
为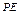 中点,求证:
中点,求证: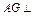 平面
平面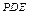 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
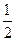 BD
BD
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
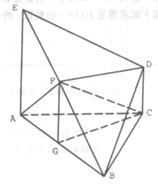
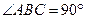 ,当E、F分别在线段AD、BC上,且
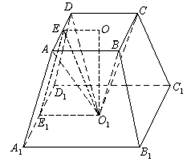
,当E、F分别在线段AD、BC上,且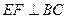 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com