
【题目】如图,在四棱锥![]() 中,平面ABCD平面PAD,
中,平面ABCD平面PAD,![]() ,
,![]() ,
,![]() ,
,![]() ,E是PD的中点.
,E是PD的中点.

![]() 证明:
证明:![]() ;
;
![]() 设
设![]() ,点M在线段PC上且异面直线BM与CE所成角的余弦值为
,点M在线段PC上且异面直线BM与CE所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
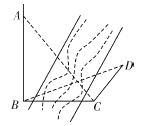
【题目】如图,为测得河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,测得点
的正东方向上,测得点![]() 的仰角为60°,再由点
的仰角为60°,再由点![]() 沿北偏东15°方向走
沿北偏东15°方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是(单位:
的高是(单位:![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
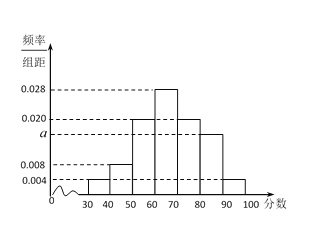
【题目】改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
(Ⅰ)求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
(Ⅱ)已知交通安全意识强的样本中男女比例为4:1,完成2×2列联表,并判断有多大把握认为交通安全意识与性别有关;
(Ⅲ)在(Ⅱ)的条件下,从交通安全意识强的驾驶员中随机抽取2人,求抽到的女性人数![]() 的分布列及期望.
的分布列及期望.
附: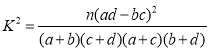 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知f(x)=|x+a|(a∈R).
(1)若f(x)≥|2x﹣1|的解集为[0,2],求a的值;
(2)若对任意x∈R,不等式f(x)+|x﹣a|≥3a﹣2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面ABCD平面PAD,
中,平面ABCD平面PAD,![]() ,
,![]() ,
,![]() ,
,![]() ,E是PD的中点.
,E是PD的中点.

![]() 证明:
证明:![]() ;
;
![]() 设
设![]() ,点M在线段PC上且异面直线BM与CE所成角的余弦值为
,点M在线段PC上且异面直线BM与CE所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆与抛物线y2=![]() x有一个相同的焦点,且该椭圆的离心率为
x有一个相同的焦点,且该椭圆的离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过点P(0,1)的直线与该椭圆交于A,B两点,O为坐标原点,若![]() ,求△AOB的面积.
,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com