
分析 (Ⅰ)求出函数的导数,各个关于a,b的方程组,解出即可;(Ⅱ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数在闭区间的最值即可.
解答 解:(Ⅰ)f′(x)=3x2-2x-a,
因为x=1时f(x)取得极值2,
所以$\left\{\begin{array}{l}f(1)=2\\ f′(1)=0\end{array}\right.$,即$\left\{\begin{array}{l}1-1-a+b=2\\ 3-2-a=0\end{array}\right.$,
解得a=1,b=3,经检验符合题意.
(Ⅱ)由(Ⅰ)知b=3,
f(x)=x3-x2-x+3,
f′(x)=3x2-2x-1,
当x∈(0,1)时f′(x)<0,f(x)单调递减;
当x∈(1,3)时,f′(x)>0,f(x)单调递增,
又f(0)=3,f(3)=18,而3<18,
故f(x)在区间[0,b]上的最大值为f(3)=18.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:解答题
 已知几何体P-ABCD如图,面ABCD为矩形,面ABCD⊥面PAB,且面PAB为正三角形,若AB=2,AD=1,E、F分别为AC、BP中点,
已知几何体P-ABCD如图,面ABCD为矩形,面ABCD⊥面PAB,且面PAB为正三角形,若AB=2,AD=1,E、F分别为AC、BP中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆的一部分 | B. | 双曲线的一部分 | C. | 抛物线的一部分 | D. | 直线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{\sqrt{a_n}\}$ | B. | $\{\frac{1}{a_n}\}$ | C. | {an2} | D. | {an+1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
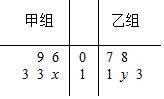 为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多$\frac{9}{5}$,则x+y的值为( )
为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多$\frac{9}{5}$,则x+y的值为( )| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com