Question

【题目】在四棱柱 中，底面 是正方形，且 ， ．

（1）求证： ；
（2）若动点 在棱 上，试确定点 的位置，使得直线 与平面 所成角的正弦值为 ．

Answer 1

【答案】
（1）证明：连接 ， ， ，

因为 ， ，
所以 和 均为正三角形，
于是 ．
设 与 的交点为 ，连接 ，则 ，
又四边形 是正方形，所以 ，
而 ，所以 平面 ．
又 平面 ，所以 ，
又 ，所以 ．
（2）解：由 ，及 ，知 ，
于是 ，从而 ，
结合 ， ，得 底面 ，
所以 、 、 两两垂直．
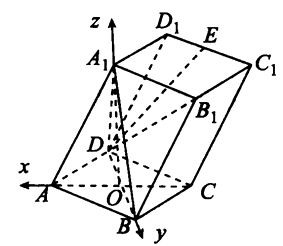
如图，以点 为坐标原点， 的方向为 轴的正方向，建立空间直角坐标系 ，
则 ， ， ， ， ， ，
， ，
由 ，易求得 ．
设 （ ），
则 ，即 ，
所以 ．
设平面 的一个法向量为 ，
由 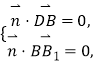得 令 ，得 ，
设直线 与平面 所成角为 ，则
，
解得 或 （舍去），
故答案为：当 为 的中点时，直线 与平面 所成角的正弦值为 ．
【解析】（1）通过线面垂直证明线线垂直.
（2）建立空间直角坐标系，设点E的坐标，由平面法向量计算线面角求得点E的坐标，从而确定点E的位置.