
【题目】已知函数![]() ,
,![]() ,
,
(1)求不等式![]() 的解集;
的解集;
(2)若对一切![]() ,均有
,均有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1){x|-2<x<4}.(2)(-∞,2].
【解析】
(1)解一元二次不等式得不等式g(x)<0的解集,(2)先化简不等式,利用变量分离法得![]() ,转化求函数
,转化求函数![]() 最小值,根据
最小值,根据![]() ,利用基本不等式求最值,即得实数m的取值范围.
,利用基本不等式求最值,即得实数m的取值范围.
解:(1)g(x)=2x2-4x-16<0,
∴(2x+4)(x-4)<0,∴-2<x<4,
∴不等式g(x)<0的解集为{x|-2<x<4}.
(2)∵f(x)=x2-2x-8.
当x>2时,f(x)≥(m+2)x-m-15恒成立,
∴x2-2x-8≥(m+2)x-m-15,
即x2-4x+7≥m(x-1).
∴对一切x>2,均有不等式![]() 成立.
成立.
而![]() =(x-1)+
=(x-1)+![]() -2
-2
≥2![]() -2=2(当x=3时等号成立).
-2=2(当x=3时等号成立).
∴实数m的取值范围是(-∞,2].


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若![]() <t<
<t<![]() ,求证:方程f(x)=0在区间(-1,0)及
,求证:方程f(x)=0在区间(-1,0)及![]() 内各有一个实数根.
内各有一个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).
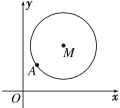
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B,C两点,且BC=OA,
求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 在平行四边形ABCD中,A(1,1),![]() =(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若![]() =(3,5),求点C的坐标;(2) 当|
=(3,5),求点C的坐标;(2) 当|![]() |=|
|=|![]() |时,求点P的轨迹.
|时,求点P的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项的和,且Sn =![]() (an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.
(an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.
①求证:数列{an }是等比数列;
②若d∈{a1 ,a2 ,a3 ,……}∩{b1 ,b2 ,b3 ,……},则称d为数列{an }和{bn }的公共项,按它们在原数列中的先后顺序排成一个新的数列{dn },求数列{dn }的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知![]() :“直线
:“直线![]() 与圆
与圆![]() 相交”;
相交”; ![]() :“
:“![]() 有一正根和一负根”.若
有一正根和一负根”.若![]() 为真,
为真, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
(2)已知椭圆![]() :
: ![]() 与圆
与圆![]() :
: ![]() ,双曲线
,双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点,它的两条渐近线恰好与圆
有相同的焦点,它的两条渐近线恰好与圆![]() 相切.求双曲线
相切.求双曲线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x|x|+bx+c,给出下列命题:①b=0,c>0时,方程f(x)=0只有一个实数根;②c=0时,y=f(x)是奇函数;③方程f(x)=0至多有两个实根.上述三个命题中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且Sn=n2﹣4n﹣5
(1)求数列{an}的通项公式;
(2)设bn=|an|,数列{bn}的前n项和为Tn, 求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com