
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若存在直线![]() ,使得对任意的
,使得对任意的![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】
(1)对函数![]() 求导,分
求导,分![]() ,
,![]() 两种情况讨论即可;
两种情况讨论即可;
(2)先由![]() 可转化为二次不等式的恒成立问题,然后构造函数
可转化为二次不等式的恒成立问题,然后构造函数![]() ,转化为对任意的
,转化为对任意的![]() ,
,![]() 恒成立问题,即可求解.
恒成立问题,即可求解.
(1)函数![]() 的定义域为
的定义域为![]() .
.
![]()
(i)若![]() ,则
,则![]() ;
;
(ii)若![]() ,则由
,则由![]() 得
得![]() ,由
,由![]() 得
得![]() ;
;
综上:当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)设存在直线![]() 满足题意.
满足题意.
(i)由![]() ,即
,即![]() 对任意的
对任意的![]() 都成立,得
都成立,得![]() ,所以
,所以![]() ,
,
(ii)令![]() ,
,
![]() ,
,
①若![]() ,则
,则![]() ,
,![]() 单调递增,
单调递增,![]() ,不合题意;
,不合题意;
②若![]() ,则
,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以![]() ,即
,即![]() ,
,
由(i)得![]() ,
,
即![]() ,
,
令![]() ,
,![]() ,
,
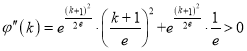 ,所以
,所以![]() 单调递增,
单调递增,
又因为![]() ,所以
,所以![]() 在
在![]() 是单调递减,
是单调递减,![]() 是单调递减,所以
是单调递减,所以![]() ,所以
,所以![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,左顶点为A,右顶点B在直线
,左顶点为A,右顶点B在直线![]() 上.
上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 运动时,判断以
运动时,判断以![]() 为直径的圆与直线PF的位置关系,并加以证明.
为直径的圆与直线PF的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时至21世纪.环境污染已经成为世界各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开小车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷6枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于4,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的分布列;
(2)由条件概率我们可以得到概率论中一个很重要公式——全概率公式.其特殊情况如下:如果事件![]() 相互对立并且
相互对立并且![]() ,则对任一事件B有
,则对任一事件B有![]() .设
.设![]() 表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
①用![]() 表示
表示![]() ;
;
②王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某次考试之后,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学、物理成绩(单位:分)对应如下表,对应散点图如图所示:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学成绩 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理成绩 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
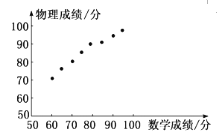
根据以上信息,则下列结论:
①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则可以判断出甲同学的物理成绩一定比乙同学的物理成绩高;
④从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则不能判断出甲同学的物理成绩一定比乙同学的物理成绩高;
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
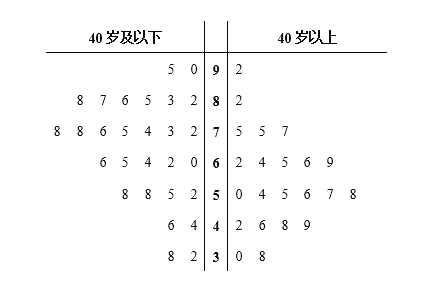
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: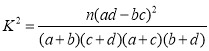 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com