
【题目】如图,直三棱柱![]() 中,底面
中,底面![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,![]() 是侧棱
是侧棱![]() 上的点.
上的点.
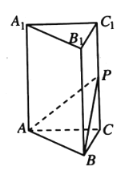
(1)若![]() ,证明:
,证明:![]() 是
是![]() 的中点;
的中点;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,由
中,由![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程以及曲线
的极坐标方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 与曲线
与曲线![]() 、曲线
、曲线![]() 在第一象限交于
在第一象限交于![]() 、
、![]() ,且
,且![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】焦点在x轴上的椭圆C:![]() 经过点
经过点![]() ,椭圆C的离心率为
,椭圆C的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.
(1)求椭圆的标准方程;
(2)若点M为![]() 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在x轴上,长轴的两个端点分别为![]() 、
、![]() .短轴的两个端点分别为
.短轴的两个端点分别为![]() ,
,![]() .菱形
.菱形![]() 的面积为
的面积为![]() ,离心率
,离心率![]() .
.
(1)求椭圆的标准方程;
(2)设![]() ,经过点M作斜率不为0的直线
,经过点M作斜率不为0的直线![]() 交椭圆C于A、B两点,若
交椭圆C于A、B两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,多面体是由底面为![]() 的直四棱柱被截面
的直四棱柱被截面![]() 所截而得到的,该直四棱柱的底面为菱形,其中
所截而得到的,该直四棱柱的底面为菱形,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
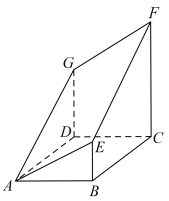
(1)求![]() 的长;
的长;
(2)求平面![]() 与底面
与底面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com