
函数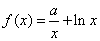 ,其中
,其中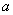 为实常数。
为实常数。
(1)讨论 的单调性;
的单调性;
(2)不等式 在
在 上恒成立,求实数
上恒成立,求实数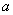 的取值范围;
的取值范围;
(3)若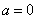 ,设
,设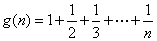 ,
,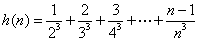
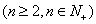 。是否存在实常数
。是否存在实常数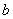 ,既使
,既使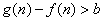 又使
又使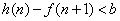 对一切
对一切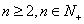 恒成立?若存在,试找出
恒成立?若存在,试找出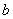 的一个值,并证明;若不存在,说明理由。
的一个值,并证明;若不存在,说明理由。
解:(1)定义域为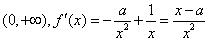 ,
,
①当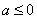 时,
时,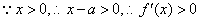 ,
,
 在定义域
在定义域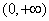 上单增;
上单增;
②当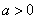 时,当
时,当 时,
时,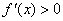 ,
, 单增;当
单增;当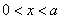 时,
时,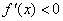 ,
, 单减。
单减。
 增区间:
增区间: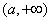 ,减区间:
,减区间: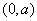 。
。
综上可知:当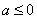 时,增区间
时,增区间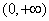 ,无减区间;当
,无减区间;当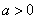 时,增区间:
时,增区间: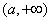 ,减区间:
,减区间: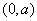 。
。
(2)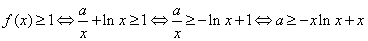 对任意
对任意 恒成立
恒成立
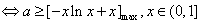 ,令
,令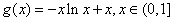 ,
,
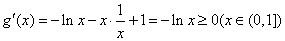 ,
,
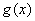 在
在 上单增,
上单增,

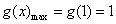 ,
,
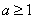 ,故
,故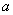 的取值范围为
的取值范围为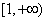 。
。
(3)存在,如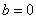 等。下面证明:
等。下面证明: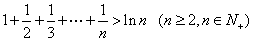
及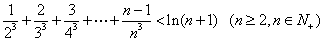 成立。
成立。
①先证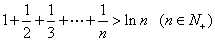 ,注意
,注意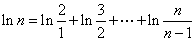 ,
,
这只要证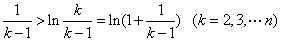 (*)即可,
(*)即可,
容易证明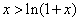 对
对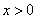 恒成立(这里证略),取
恒成立(这里证略),取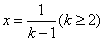 即可得上式成立。
即可得上式成立。
让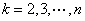 分别代入(*)式再相加即证:
分别代入(*)式再相加即证: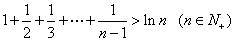 ,
,
于是 。
。
②再证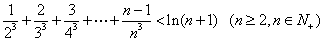 ,
,
法一: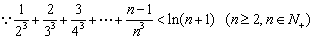
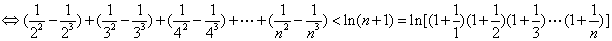
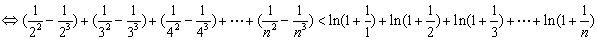
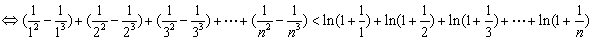 只须证
只须证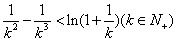 ,构造证明函数不等式:
,构造证明函数不等式: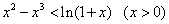 ,
,
令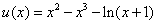 ,
, ,当
,当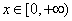 时,
时,
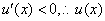 在
在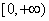 上单调递减,又
上单调递减,又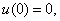
 当
当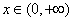 时,恒有
时,恒有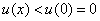 ,即
,即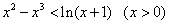 恒成立。
恒成立。
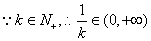 ,取
,取 ,则有
,则有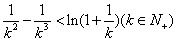 ,
,
让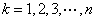 分别代入上式再相加即证:
分别代入上式再相加即证:
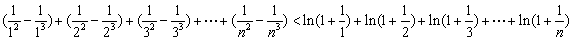 ,
,
即证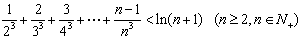 。
。
法二: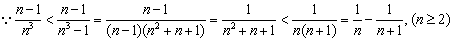 ,
,
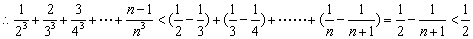 ,
,
又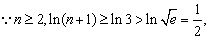 故不等式成立。
故不等式成立。
(注意:此题也可用数学归纳法!)


科目:高中数学 来源: 题型:
某段城铁线路上依次有A,B,C三站,AB=5km,BC=3km在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行时,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度vkm/h,匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(1)分别写出列车在B、C两站的运行误差;
(2)若要求列车在B,C两站的运行误差之和不超过2分钟,求v的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
等比数列{an}中,a1=512,公比q=- ,用Ⅱn
,用Ⅱn 表示它的前n项之积:Ⅱn=a1·a2…an,则Ⅱ1,Ⅱ2…中最大的是 ( )
表示它的前n项之积:Ⅱn=a1·a2…an,则Ⅱ1,Ⅱ2…中最大的是 ( )
A.Ⅱ11 B.Ⅱ10 C.Ⅱ9 D.Ⅱ8
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一条曲线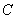 在
在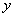 轴右侧,
轴右侧,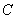 上每一点到点
上每一点到点 的距离减去它到
的距离减去它到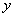 轴距离的差都是1。
轴距离的差都是1。
(1)求曲线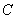 的方程;
的方程;
(2)设直线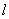 交曲线
交曲线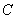 于
于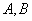 两点,线段
两点,线段 的中点为
的中点为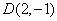 ,求直线
,求直线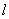 的一般式方程。
的一般式方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}是逐项递减的等比数列,其首项a1 < 0,则其公比q的取值范围是( )
A.(-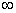 ,-1) B.(-1,0)
,-1) B.(-1,0)
C.(0,1) D.(1,+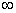 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列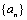 是首项大于零的等比数列,则“
是首项大于零的等比数列,则“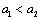 ”是“数列
”是“数列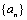 是递增数列”的( )
是递增数列”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com