已知f(x)=log2(4x+1)+2kx(x∈R)是偶函数.
(1)求实数k的值;
(2)若关于x的方程f(x)-m=0有解,求实数m的取值范围.
解:(1)∵函数f(x)=log
2(4
x+1)+2kx(k∈R)是偶函数
∴f(-x)=log
2(4
-x+1)-2kx=f(x)=log
2(4
x+1)+2kx恒成立
即log
2(4
x+1)-2x-2kx=log
2(4
x+1)+2kx恒成立
解得k=-

;
(2)由(1)知,f(x)=log
2(4
x+1)-x
∴f(x)-m=0等价于m=log
2(4
x+1)-x
∵log
2(4
x+1)-x=
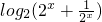
≥1
∴要使方程f(x)-m=0有解,m的取值范围为m≥1.
分析:(1)根据函数f(x)是偶函数建立等式关系,化简可得实数k的值;
要使方程f(x)-m=0有解,转化成求函数的值域,将m分离出来,利用基本不等式,即可求实数m的取值范围.
点评:本题考查的知识点是函数与方程的综合运用,偶函数,其中根据偶函数的定义求出k值,进而得到函数f(x)的解析式,是解答的关键.

 ;
;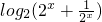 ≥1
≥1

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案