
【题目】某校在高二年级开展了体育分项教学活动,将体育课分为大球(包括篮球、排球、足球)、小球(包括乒乓球、羽毛球)、田径、体操四大项(以下简称四大项,并且按照这个顺序).为体现公平,学校规定时间让学生在电脑上选课,据初步统计,在全年级980名同学中,有意申报四大项的人数之比为3:2:1:1,而实际上由于受多方面条件影响,最终确定的四大项人数必须控制在2:1:3:1,选课不成功的同学由电脑自动调剂到田径类.
(Ⅰ)随机抽取一名同学,求该同学选课成功(未被调剂)的概率;
(Ⅱ)某小组有五名同学,有意申报四大项的人数分别为2、1、1、1,记最终确定到田径类的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为 ![]() ,直线l的参数方程为
,直线l的参数方程为 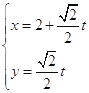 (t为常数,t∈R)
(t为常数,t∈R)
(1)求直线l的普通方程和圆C的直角坐标方程;
(2)求直线l与圆C相交的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 、
、![]() 为椭圆的左右顶点,焦点到短轴端点的距离为2,
为椭圆的左右顶点,焦点到短轴端点的距离为2, ![]() 、
、![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 、
、![]() 的两点,且直线
的两点,且直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的2倍.
斜率的2倍.

(Ⅰ)求证:直线![]() 与直线
与直线![]() 的斜率乘积为定值;
的斜率乘积为定值;
(Ⅱ)求三角形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学有A、B、C三个不同的校区,其中A校区有4000人,B校区有3000人,C校区有2000人,采用按校区分层抽样的方法,从中抽取900人参加一项活动,则A、B、C校区分别抽取( )
A.400人、300人、200人
B.350人、300人、250人
C.250人、300人、350人
D.200人、300人、400人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
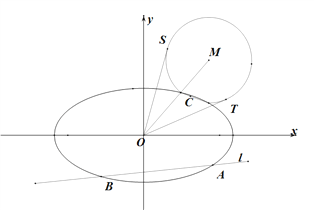
(Ⅱ)如图,动直线![]() :
: ![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,
, ![]() 的半径为
的半径为![]() ,
, ![]() 是
是![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .求
.求![]() 的最大值,并求取得最大值时直线
的最大值,并求取得最大值时直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,函数f(x)=loga ![]() .
.
(1)求f(x)的定义域D及其零点;
(2)设g(x)=mx2﹣2mx+3,当a>1时,若对任意x1∈(﹣∞,﹣1],存在x2∈[3,4],使得f(x1)≤g(x2),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“全面二孩”政策推行,我市将迎来生育高峰。今年新春伊始,泉城各医院产科就已经是一片忙碌至今热度不减。卫生部门进行调查统计期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中10个是“二孩”宝宝;
(1)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询,
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(II)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
P(k≥k市) | 0.40 | 0.25 | 0.15 | 0.10 |
k市 | 0.708 | 1.323 | 2.072 | 2.706 |
K2=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com