
【题目】随着“全面二孩”政策推行,我市将迎来生育高峰。今年新春伊始,泉城各医院产科就已经是一片忙碌至今热度不减。卫生部门进行调查统计期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中10个是“二孩”宝宝;
(1)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询,
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(II)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
P(k≥k市) | 0.40 | 0.25 | 0.15 | 0.10 |
k市 | 0.708 | 1.323 | 2.072 | 2.706 |
K2=![]()
【答案】(I)①2个;②![]() (II)没有85%的把握认为一孩、二孩宝宝的出生于医院有关。
(II)没有85%的把握认为一孩、二孩宝宝的出生于医院有关。
【解析】试题分析:
(1)由题意结合抽样比可得在市第一医院出生的一孩宝宝中抽取2个,这两个宝宝恰出生不同医院且均属“二孩”的概率是![]() ;
;
(2)由题意可求得K2≈1.944<2.072,故没有85%的把握认为一孩、二孩、孩宝宝的出生与医院有关。
试题解析:
(I)①由分层抽样知在市第一医院出生的宝宝有7x![]() =4个,其中一孩宝宝有2个。
=4个,其中一孩宝宝有2个。
②在抽取7个宝宝中,市一院出生的一孩宝宝2人分别记为A1,B1,二孩宝宝2人,分别记
为a1,b1,妇幼保健院出生的一孩宝宝2人,分别记为A2,B2,二孩宝宝1人,记为a2,从7人中抽取2人的一切可能结果所组成的基本事件空间为
Ω={(A1,B1),(A1,a1),(A1,b1)(A1,A2),(A1,B2),(A1,a1),(B1,a1),(B1,b1),(B1,A2),(B1,B2),(B1,a2),(a1,b1),(a1,A2),(a1,B2),(a1,a=2),(b1,A2),(b1,B2),(b1,a2),(A2,B2),(A2,a2),(B2,a=2)}
可用A表示:“两个宝宝掐出生不同医院且均属二孩”,则A={(a1,a2),(b1,a2)}
∴P(A)=![]()
(II)2x2列联表
一孩 | 二孩 | 合计 | |
第一医院 | 20 | 20 | 40 |
妇幼保健院 | 20 | 10 | 30 |
合计 | 40 | 30 | 70 |
K2=![]() ≈1.944<2.072,故没有85%的把握认为一孩、二孩、孩宝宝的出生与医院有关。
≈1.944<2.072,故没有85%的把握认为一孩、二孩、孩宝宝的出生与医院有关。


科目:高中数学 来源: 题型:
【题目】某校在高二年级开展了体育分项教学活动,将体育课分为大球(包括篮球、排球、足球)、小球(包括乒乓球、羽毛球)、田径、体操四大项(以下简称四大项,并且按照这个顺序).为体现公平,学校规定时间让学生在电脑上选课,据初步统计,在全年级980名同学中,有意申报四大项的人数之比为3:2:1:1,而实际上由于受多方面条件影响,最终确定的四大项人数必须控制在2:1:3:1,选课不成功的同学由电脑自动调剂到田径类.
(Ⅰ)随机抽取一名同学,求该同学选课成功(未被调剂)的概率;
(Ⅱ)某小组有五名同学,有意申报四大项的人数分别为2、1、1、1,记最终确定到田径类的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=27,定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)确定y=g(x),y=f(x)的解析式;
(2)若h(x)=kx﹣g(x)在(0,1)上有零点,求k的取值范围;
(3)若对任意的t∈(1,4),不等式f(2t﹣3)+f(t﹣k)>0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=3,且公差d≠0,其前n项和为Sn , 且a1 , a4 , a13分别是等比数列{bn}的b2 , b3 , b4 . (Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)证明 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
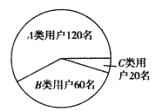
【题目】2016年10月,继微信支付对提现转账收费后,支付宝也开始对提现转账收费,随着这两大目前用户使用粘度最高的第三方支付开始收费,业内人士分析,部分对价格敏感的用户或将回流至传统银行体系,某调查机构对此进行调查,并从参与调查的数万名支付宝用户中随机选取200人,把这200人分为3类:认为使用支付宝方便,仍使用支付宝提现转账的用户称为“![]() 类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“
类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“![]() 类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“
类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“![]() 类用户”,各类用户的人数如图所示:
类用户”,各类用户的人数如图所示:
同时把这200人按年龄分为青年人组与中老年人组,制成如图所示的![]() 列联表:
列联表:
| 非 | 合计 | |
青年 | 20 | ||
中老年 | 40 | ||
合计 | 200 |
(Ⅰ)完成![]() 列联表并判断是否有99.5%的把握认为“
列联表并判断是否有99.5%的把握认为“![]() 类用户与年龄有关”;
类用户与年龄有关”;
(Ⅱ)从这200人中按![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中
类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户均存在的概率;
类用户均存在的概率;
(Ⅲ)把频率作为概率,从支付宝所有用户(人数很多)中随机抽取3人,用![]() 表示所选3人中
表示所选3人中![]() 类用户的人数,求
类用户的人数,求![]() 的分布列与期望.
的分布列与期望.
附:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x3﹣
x3﹣ ![]() ax2+(a﹣1)x+1在区间(2,3)内为减函数,在区间(5,+∞)为增函数,则实数a的取值范围是( )
ax2+(a﹣1)x+1在区间(2,3)内为减函数,在区间(5,+∞)为增函数,则实数a的取值范围是( )
A.[3,4]
B.[5,7]
C.[4,6]
D.[7,8]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com