
分析 根据二项式展开式的通项写出展开式中x2项的系数,列方程求出a的值,再求定积分的值.
解答 解:设${({a{x^2}-\frac{1}{{\sqrt{x}}}})^6}$展开式的通项为:
${T_{k+1}}=C_6^k{({a{x^2}})^{6-k}}{({-{x^{-\frac{1}{2}}}})^k}=C_6^k{a^{6-k}}{({-1})^k}{x^{12-\frac{5}{2}k}}$,
令$12-\frac{5}{2}k=2$,求得k=4;
于是展开式中x2项的系数为$C_6^k{a^2}=15{a^2}$,
则15a2=60,
注意到a>0,求得a=2;
所以${∫}_{-1}^{a}$(x2-2x)dx=${∫}_{-1}^{2}$(x2-2x)dx
=($\frac{1}{3}$x3-x2)${|}_{-1}^{2}$
=($\frac{1}{3}$×23-22)-[$\frac{1}{3}$×(-1)3-(-1)2]
=-$\frac{4}{3}$+$\frac{4}{3}$
=0.
故答案为:0.
点评 本题考查了二项式展开式的应用问题,也考查了定积分的计算问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
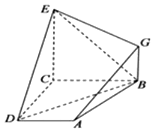 如图,已知四边形ABCD和BCGE均为直角梯形,AD∥BC,CE∥BG且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCGE,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCGE均为直角梯形,AD∥BC,CE∥BG且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCGE,BC=CD=CE=2AD=2BG=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com