
分析 (1)分类讨论,解不等式,综合讨论结果,可得答案;
(2)根据绝对值的性质,求出|x+1|-|a-x|的最大值,进而可得满足条件的实数a的取值范围.
解答 解:(1)不等式|2x+1|-f(x)<1,即不等式|2x+1|-|x+1|<1,
x≤-1,不等式化为-2x-1+x+1<1,∴x>-1,无解;
-1<x<-$\frac{1}{2}$,不等式化为-2x-1-x-1<1,∴x>-1,∴-1<x<-$\frac{1}{2}$;
x≥-$\frac{1}{2}$,不等式化为2x+1-x-1<1,∴x<1,∴-$\frac{1}{2}$≤x<1,
综上所述,不等式的解集为{x|-1<x<1};
(2)|x+1|-|a-x|≤|(x+1)+(a-x)|=|a+1|,
若关于x的不等式f(x)≥|a-x|+2的解集为非空集合,则|a+1|≥2,
解得:a∈(-∞,-3)∪(1,+∞).
点评 本题考查的知识点是分段函数的应用,绝对值三角不等式,难度中档.


科目:高中数学 来源: 题型:填空题
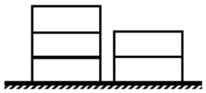 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是10(用数字作答).
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是10(用数字作答).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
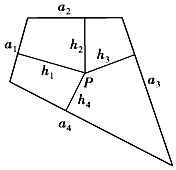 如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )
如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )| A. | $\frac{V}{2K}$ | B. | $\frac{2V}{K}$ | C. | $\frac{3V}{K}$ | D. | $\frac{V}{3K}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )
中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )| A. | 2000 | B. | 2800 | C. | 3000 | D. | 6000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com