练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
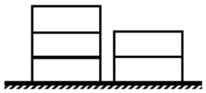
    14．如图所示，某货场有两堆集装箱，一堆2个，一堆3个，现需要全部装运，每次只能从其中一堆取最上面的一个集装箱，则在装运的过程中不同取法的种数是10（用数字作答）．

    分析 根据题意，假设左边的积木从上至下依次为1、2、3，右边的积木从上至下依次为4、5，分析可得必须先取1或4，据此分2种情况讨论，分别列举2种情况下的取法数目，由分类计数原理计算可得答案．

    解答 解：根据题意，假设左边的积木从上至下依次为1、2、3，右边的积木从上至下依次为4、5，
    分2种情况讨论：
    若先取1，有12345、12453、12435、14235、14253、14523，共6种取法；
    若先取4，有45123、41523、41253、41235，共4种取法；
    则一共有6+4=10中不同的取法；
    故答案为：10．

    点评 本题考查计数原理的应用，关键是依据题意，正确进行分类讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．设向量$\overrightarrow{a}$=（2，0），$\overrightarrow{b}$=（1，1），则下列结论中正确的是（　　）
    A．|$\overrightarrow{a}$|=|$\overrightarrow{b}$|B．$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$C．$\overrightarrow{a}$⊥$\overrightarrow{b}$D．（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{b}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

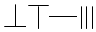    5．中国有个名句“运筹帷幄之中，决胜千里之外．”其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图所示），表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推．例如6613用算筹表示就是，则9117用算筹可表示为（　　）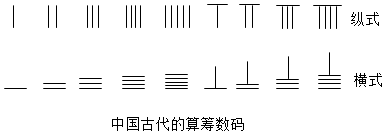
    A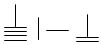．B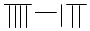．C．D．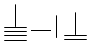

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．对任意的正整数n，以及任意n个互不相同的正整数a1，a2，…，an，若不等式${（{\frac{1}{a_1}}）^λ}+{（{\frac{1}{a_2}}）^λ}+…+{（{\frac{1}{a_n}}）^λ}＜2$恒成立，求整数λ的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

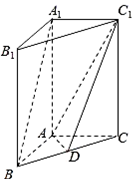    9．如图，在直三棱锥A1B1C1-ABC，AB⊥AC，AB=AC=2，AA1=4，点D是BC的中点．
    （1）求异面直线A1B与C1D所成角的余弦值；
    （2）求平面ADC1与平面A1BA所成的二面角（是指不超过90°的角）的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

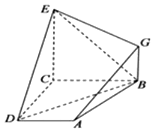    19．如图，已知四边形ABCD和BCGE均为直角梯形，AD∥BC，CE∥BG且∠BCD=∠BCE=$\frac{π}{2}$，平面ABCD⊥平面BCGE，BC=CD=CE=2AD=2BG=2．
    （1）求证：AG∥平面BDE；
    （2）求三棱锥G-BDE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

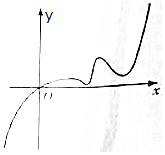    6．已知函数f（x）的定义域为R，且f（2）=2，又函数f（x）的导函数y=f′（x）的图象如图所示，若两个正数a、b满足f（2a+b）＜2，则$\frac{b+2}{a+2}$的取值范围是（　　）
    A．（$\frac{2}{3}$，2）B．（-∞，$\frac{2}{3}$）∪（2，+∞）C．（2，+∞）D．（-∞，$\frac{2}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=|x+1|．
    （1）求不等式|2x+1|-f（x）＜1的解集；
    （2）若关于x的不等式f（x）≥|a-x|+2的解集为非空集合，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知ai＞0（i=1，2，3，…，n），观察下列不等式：$\frac{{{a_1}+{a_2}}}{2}≥\sqrt{{a_1}{a_2}}$；$\frac{{{a_1}+{a_2}+{a_3}}}{3}≥\root{3}{{{a_1}{a_2}{a_3}}}$；$\frac{{{a_1}+{a_2}+{a_3}+{a_4}}}{4}≥\root{4}{{{a_1}{a_2}{a_3}{a_4}}}$；
    …
    照此规律，当n∈N*（n≥2）时，$\frac{{{a_1}+{a_2}+…+{a_n}}}{n}≥$$\root{n}{{{a_1}{a_2}…{a_n}}}$．

    查看答案和解析>>

    同步练习册答案