
ЗжЮі гЩЬтвтЃЌжЊзѓБпУПвЛИіЪНзгЪЧЫуЪѕЦНОљЪ§ЃЌгвБпЕФЪНзгЪЧМИКЮЦНОљЪ§ЃЌМДМИИіЪ§ЫуЪѕЦНОљЪ§ВЛаЁгкЫќУЧЕФМИКЮЦНОљЪ§ЃЌМДПЩЕУГіНсТлЃЎ
НтД№ НтЃКгЩЬтвтЃЌжЊзѓБпУПвЛИіЪНзгЪЧЫуЪѕЦНОљЪ§ЃЌгвБпЕФЪНзгЪЧМИКЮЦНОљЪ§ЃЌМДМИИіЪ§ЫуЪѕЦНОљЪ§ВЛаЁгкЫќУЧЕФМИКЮЦНОљЪ§ЃЎ
ЙщФЩЭЦВтЕБnЁЪN*ЃЈnЁн2ЃЉЪБЃЌ$\frac{{{a_1}+{a_2}+Ё+{a_n}}}{n}Ён$$\root{n}{{{a_1}{a_2}Ё{a_n}}}$ЃЎ
ЙЪД№АИЮЊЃК$\root{n}{{{a_1}{a_2}Ё{a_n}}}$ЃЎ
ЕуЦР БОЬтПМВщЙщФЩЭЦРэЃЌПМВщбЇЩњЗжЮіНтОіЮЪЬтЕФФмСІЃЌБШНЯЛљДЁЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
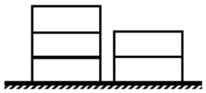 ШчЭМЫљЪОЃЌФГЛѕГЁгаСНЖбМЏзАЯфЃЌвЛЖб2ИіЃЌвЛЖб3ИіЃЌЯжашвЊШЋВПзАдЫЃЌУПДЮжЛФмДгЦфжавЛЖбШЁзюЩЯУцЕФвЛИіМЏзАЯфЃЌдђдкзАдЫЕФЙ§ГЬжаВЛЭЌШЁЗЈЕФжжЪ§ЪЧ10ЃЈгУЪ§зжзїД№ЃЉЃЎ
ШчЭМЫљЪОЃЌФГЛѕГЁгаСНЖбМЏзАЯфЃЌвЛЖб2ИіЃЌвЛЖб3ИіЃЌЯжашвЊШЋВПзАдЫЃЌУПДЮжЛФмДгЦфжавЛЖбШЁзюЩЯУцЕФвЛИіМЏзАЯфЃЌдђдкзАдЫЕФЙ§ГЬжаВЛЭЌШЁЗЈЕФжжЪ§ЪЧ10ЃЈгУЪ§зжзїД№ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
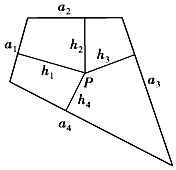 ШчЭМЫљЪОЃЌУцЛ§ЮЊSЕФЦНУцЭЙЫФБпаЮЕФЕкiЬѕБпЕФБпГЄЮЊaiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌДЫЫФБпаЮФкдквЛЕуPЕНЕкiЬѕБпЕФОрРыМЧЮЊhiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌШє$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=kЃЌдђh1+3h2+5h3+7h4=$\frac{2S}{k}$ЃЎРрБШвдЩЯаджЪЃЌЬхЛ§ЮЊVЕФШ§РтзЖЕФЕкiИіУцЕФУцЛ§МЧЮЊSiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌДЫШ§РтзЖФкШЮвЛЕуQЕНЕкiИіУцЕФОрРыМЧЮЊHiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌШє$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=KЃЌH1+3H2+5H3+7H4=ЃЈЁЁЁЁЃЉ
ШчЭМЫљЪОЃЌУцЛ§ЮЊSЕФЦНУцЭЙЫФБпаЮЕФЕкiЬѕБпЕФБпГЄЮЊaiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌДЫЫФБпаЮФкдквЛЕуPЕНЕкiЬѕБпЕФОрРыМЧЮЊhiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌШє$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=kЃЌдђh1+3h2+5h3+7h4=$\frac{2S}{k}$ЃЎРрБШвдЩЯаджЪЃЌЬхЛ§ЮЊVЕФШ§РтзЖЕФЕкiИіУцЕФУцЛ§МЧЮЊSiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌДЫШ§РтзЖФкШЮвЛЕуQЕНЕкiИіУцЕФОрРыМЧЮЊHiЃЈi=1ЃЌ2ЃЌ3ЃЌ4ЃЉЃЌШє$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=KЃЌH1+3H2+5H3+7H4=ЃЈЁЁЁЁЃЉ| AЃЎ | $\frac{V}{2K}$ | BЃЎ | $\frac{2V}{K}$ | CЃЎ | $\frac{3V}{K}$ | DЃЎ | $\frac{V}{3K}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | [0ЃЌ+ЁоЃЉ | BЃЎ | [1ЃЌ3] | CЃЎ | ЃЈ-1ЃЌ-$\frac{1}{3}$] | DЃЎ | [-1ЃЌ-$\frac{1}{3}$] |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 жаЙњЕФМЦСПЕЅЮЛПЩвдзЗЫнЕН4000ЖрФъЧАЕФЪЯзхЩчЛсФЉЦкЃЌЙЋдЊЧА221ФъЃЌЧиЭѕЭГвЛжаЙњКѓЃЌАфВМЭЌвЛЖШСПКтЕФкЏЪщВЂжЦЗЂСЫГЩЬзЕФШЈКтКЭШнСПБъзМЦїЃЎЯТЭМЪЧЙХДњЕФвЛжжЖШСПЙЄОпЁАЖЗЁБЃЈЮоИЧЃЌВЛМЦСПКёЖШЃЉЕФШ§ЪгЭМЃЈЦфе§ЪгЭМКЭВрЪгЭМЮЊЕШбќЬнаЮЃЉЃЌдђДЫЁАЖЗЁБЕФЬхЛ§ЮЊЃЈЕЅЮЛЃКСЂЗНРхУзЃЉЃЈЁЁЁЁЃЉ
жаЙњЕФМЦСПЕЅЮЛПЩвдзЗЫнЕН4000ЖрФъЧАЕФЪЯзхЩчЛсФЉЦкЃЌЙЋдЊЧА221ФъЃЌЧиЭѕЭГвЛжаЙњКѓЃЌАфВМЭЌвЛЖШСПКтЕФкЏЪщВЂжЦЗЂСЫГЩЬзЕФШЈКтКЭШнСПБъзМЦїЃЎЯТЭМЪЧЙХДњЕФвЛжжЖШСПЙЄОпЁАЖЗЁБЃЈЮоИЧЃЌВЛМЦСПКёЖШЃЉЕФШ§ЪгЭМЃЈЦфе§ЪгЭМКЭВрЪгЭМЮЊЕШбќЬнаЮЃЉЃЌдђДЫЁАЖЗЁБЕФЬхЛ§ЮЊЃЈЕЅЮЛЃКСЂЗНРхУзЃЉЃЈЁЁЁЁЃЉ| AЃЎ | 2000 | BЃЎ | 2800 | CЃЎ | 3000 | DЃЎ | 6000 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 вбжЊЭждВEЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉОЙ§ЕуЃЈ$\frac{\sqrt{5}}{2}$ЃЌ$\frac{\sqrt{3}}{2}$ЃЉЃЌРыаФТЪЮЊ$\frac{2\sqrt{5}}{5}$ЃЌЕуOЮЛзјБъдЕуЃЎ
вбжЊЭждВEЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉОЙ§ЕуЃЈ$\frac{\sqrt{5}}{2}$ЃЌ$\frac{\sqrt{3}}{2}$ЃЉЃЌРыаФТЪЮЊ$\frac{2\sqrt{5}}{5}$ЃЌЕуOЮЛзјБъдЕуЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com