
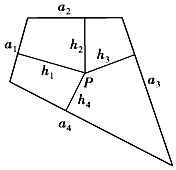
 ��ͼ��ʾ�����ΪS��ƽ���ı��εĵ�i���ߵı߳�Ϊai��i=1��2��3��4�������ı�������һ��P����i���ߵľ����Ϊhi��i=1��2��3��4������$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k����h1+3h2+5h3+7h4=$\frac{2S}{k}$������������ʣ����ΪV�������ĵ�i����������ΪSi��i=1��2��3��4��������������һ��Q����i����ľ����ΪHi��i=1��2��3��4������$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K��H1+3H2+5H3+7H4=��������
��ͼ��ʾ�����ΪS��ƽ���ı��εĵ�i���ߵı߳�Ϊai��i=1��2��3��4�������ı�������һ��P����i���ߵľ����Ϊhi��i=1��2��3��4������$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k����h1+3h2+5h3+7h4=$\frac{2S}{k}$������������ʣ����ΪV�������ĵ�i����������ΪSi��i=1��2��3��4��������������һ��Q����i����ľ����ΪHi��i=1��2��3��4������$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K��H1+3H2+5H3+7H4=��������| A�� | $\frac{V}{2K}$ | B�� | $\frac{2V}{K}$ | C�� | $\frac{3V}{K}$ | D�� | $\frac{V}{3K}$ |
���� ������������ɷָ�Ϊ4����֪������ߵ�С������������ɵó����ۣ�
��� �⣺���������������ʽV=$\frac{1}{3}Sh$
�ã�$\frac{1}{3}$S1H1+$\frac{1}{3}$S2H2+$\frac{1}{3}$S3H3+$\frac{1}{3}$S4H4=V��
��S1H1+S2H2+S3H3+S4H4=3V��
��$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=k��
��H1+3H2+5H3+7H4=$\frac{3V}{k}$��
��ѡC��
���� ������Ҫ�������������������������˼���������������������Ĺؼ�������������������壬������������ķ�����ƽ�漸�ε�������ۣ�����ͨ����ȵķ������õ����弸������Ӧ�Ľ��ۣ���Ȼ����ȵõ��Ľ����Ƿ���ȷ��������Ҫͨ��֤�����ܼ��Կ϶��ģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2�� | B�� | ��2��0�� | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
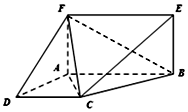 ��ͼ����֪AF��ƽ��ABCD���ı���ABEFΪ���Σ��ı���ABCDΪֱ�����Σ���DAB=90�㣬AB��CD��AD=AF=CD=2��AB=4��
��ͼ����֪AF��ƽ��ABCD���ı���ABEFΪ���Σ��ı���ABCDΪֱ�����Σ���DAB=90�㣬AB��CD��AD=AF=CD=2��AB=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1�� | B�� | ��1��+�ޣ� | C�� | ��-�ޣ�2�� | D�� | ��2��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com