
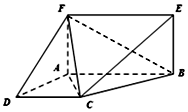
 如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.分析 (I)由AF∥BE,BE?平面BCE,AF?平面BCE,得AF∥平面BCE.
(II)过C作CM⊥AB,垂足为M,由AC2+BC2=AB2,得AC⊥BC;再证BE⊥AC,即可得到AC⊥平面BCE.
(III∠FCA为二面角F-BC-D平面角的平面角,在Rt△AFC中,求得二面角F-BC-D平面角的余弦值
解答 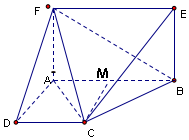 解:(I)因为四边形ABEF为矩形,所以AF∥BE,BE?平面BCE,AF?平面BCE,
解:(I)因为四边形ABEF为矩形,所以AF∥BE,BE?平面BCE,AF?平面BCE,
所以AF∥平面BCE.
(II)过C作CM⊥AB,垂足为M,
因为AD⊥DC所以四边形ADCM为矩形.所以AM=MB=2,又因为AD=2,AB=4所以AC=2$\sqrt{2}$,CM=2,BC=2$\sqrt{2}$
所以AC2+BC2=AB2,所以AC⊥BC;
因为AF⊥平面ABCD,AF∥BE,所以BE⊥平面ABCD,所以BE⊥AC,
又因为BE?平面BCE,BC?平面BCE,BE∩BC=B所以AC⊥平面BCE.
(III)∵FA⊥面ABCD,AC⊥BC,∴∠FCA为二面角F-BC-D平面角的平面角,在Rt△AFC中,cos∠ACF=$\frac{AF}{FC}=\frac{2\sqrt{2}}{2\sqrt{3}}=\frac{\sqrt{6}}{3}$
二面角F-BC-D平面角的余弦值为$\frac{\sqrt{6}}{3}$
点评 本题考查了空间线面平行、线面垂直的判定,及几何法求二面角,属于基础题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
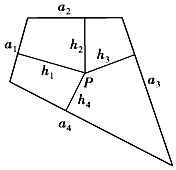 如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )
如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )| A. | $\frac{V}{2K}$ | B. | $\frac{2V}{K}$ | C. | $\frac{3V}{K}$ | D. | $\frac{V}{3K}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [1,3] | C. | (-1,-$\frac{1}{3}$] | D. | [-1,-$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )
中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )| A. | 2000 | B. | 2800 | C. | 3000 | D. | 6000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com