
| A. | 6 | B. | 5 | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
分析 由球的球心在四棱锥P-的高上,把空间问题平面化,
作出过正四棱锥的高作组合体的轴截面,利用平面几何知识即可求出高.
解答 解:由题意,四棱锥P-ABCD是正四棱锥,球的球心O在四棱锥的高PH上;
过正四棱锥的高作组合体的轴截面如图所示:
其中PE,PF是斜高,A为球面与侧面的切点,
设PH=h,由几何体可知,RT△PAO∽RT△PHF,
∴$\frac{OA}{FH}$=$\frac{PO}{PF}$,即$\frac{1}{3}$=$\frac{h-1}{\sqrt{{h}^{2}{+3}^{2}}}$,
解得h=$\frac{9}{4}$.
故选:D.
点评 本题主要考查了球内切多面体、几何体的结构特征,把空间问题平面化,是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | b>a>c | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
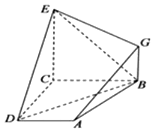 如图,已知四边形ABCD和BCGE均为直角梯形,AD∥BC,CE∥BG且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCGE,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCGE均为直角梯形,AD∥BC,CE∥BG且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCGE,BC=CD=CE=2AD=2BG=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
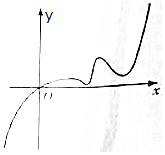 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )| A. | ($\frac{2}{3}$,2) | B. | (-∞,$\frac{2}{3}$)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
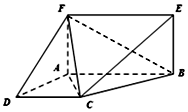 如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com