
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,2) | D. | (2,+∞) |
分析 可构造函数令g(x)=exf(x)-2ex-4,然后求导,根据条件即可得出g′(x)>0,进而得出函数g(x)在R上单调递增,并求出g(1)=0,这样便可求出原不等式的解集.
解答 解:令g(x)=exf(x)-2ex-4,g′(x)=exf(x)+exf′(x)-2ex=ex[f(x)+f′(x)-2];
∵f(x)+f′(x)>2;
∴g′(x)>0;
∴g(x)在R上单调递增;
$f(1)=2+\frac{4}{e}$;
∴$g(1)=e(2+\frac{4}{e})-2e-4=0$;
∴x>1时,g(x)>0;
∴原不等式的解集为(1,+∞).
故选B.
点评 考查导函数的概念,构造函数解决问题的方法,积的函数的求导公式,函数导数符号和函数单调性的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
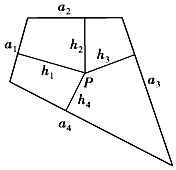 如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )
如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )| A. | $\frac{V}{2K}$ | B. | $\frac{2V}{K}$ | C. | $\frac{3V}{K}$ | D. | $\frac{V}{3K}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
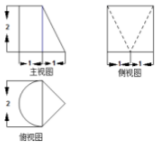
 中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )
中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )| A. | 2000 | B. | 2800 | C. | 3000 | D. | 6000 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π+$\frac{4}{3}$ | B. | $\frac{π}{3}$+4 | C. | $\frac{2}{3}$π+$\frac{4}{3}$ | D. | $\frac{2}{3}$π+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{7}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com