
利用数学归纳法证明“(n+1)(n+2)…(n+n)=2n×1×3×…×(2n﹣1),n∈N*”时,从“n=k”变到“n=k+1”时,左边应增乘的因式是( )
A.2k+1 B.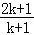 C.
C.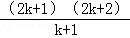 D.
D.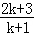
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:选择题
下列几个不同进制数最大的是( )
A.3(10) B.11(2) C.3(8) D.11(3)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证明等式 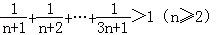 的过程中,由n=k递推到n=k+1时不等式左边( )
的过程中,由n=k递推到n=k+1时不等式左边( )
A.增加了项 B.增加了项 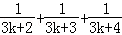
C.增加了项 D.以上均不对
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═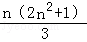 时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
A.(k+1)2+2k2 B.(k+1)2+k2
C.(k+1)2 D.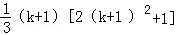
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
(2012•成都一模)在用数学归纳法证明f(n)= +
+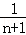 +…+
+…+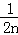 <1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
<1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
A.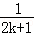 +
+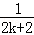 B.
B.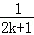 +
+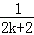 ﹣
﹣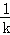 C.
C.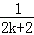 ﹣
﹣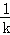 D.
D.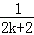 ﹣
﹣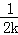
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷(解析版) 题型:填空题
(2014•宜昌三模)若a,b,c为正实数且满足a+2b+3c=6,则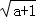 +
+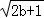 +
+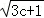 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷(解析版) 题型:填空题
(2009•惠州模拟)设x+y+z=2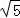 ,则m=x2+2y2+z2的最小值为 .
,则m=x2+2y2+z2的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com